题目内容
(2012•武昌区模拟)(坐标系与参数方程)在直角坐标系中,以原点为极点,x轴的正半轴为极轴建极坐标系,两种坐标系取相同的单位长度.已知曲线C:psin2θ=2acosθ(a>0),过点P(-2,-4)的直线l的参数方程为
,直线l与曲线C分别交于M、N.若|PM|、|MN|、|PN|成等比数列,则实数a的值为
|
1
1
.分析:把参数方程化为普通方程,把极坐标方程化为直角坐标方程,联立方程组利用根与系数的关系求出x1+x2=4+2a,x1•x2=4.再根据由|PM|、|MN|、|PN|成等比数列可得
2(x1-x 2)2=
|x1+2|•
|x2+2|,由此求得实数a的值.
2(x1-x 2)2=
| 2 |
| 2 |
解答:解:曲线C:psin2θ=2acosθ(a>0),即 ρ2sin2θ=2aρcosθ,即 y2=2ax. 直线l的参数方程
,即 x-y-2=0.
设M(x1,x1-2),N(x2,x2-2),则由
可得 x2-(4+2a)x+4=0,∴x1+x2=4+2a,x1•x2=4.
由|PM|、|MN|、|PN|成等比数列,可得|MN|2=|PM||PN|.
∴2(x1-x 2)2=
•
,化简可得 2(x1-x 2)2=
|x1+2|•
|x2+2|.
即 (x1+x 2)2-4x1•x2=|x1•x2+2(x1+x2)+4|,∴(4+2a)2-16=|4+2(4+2a)+4|,
解得 a=1,
故答案为 1.
|
设M(x1,x1-2),N(x2,x2-2),则由
|
由|PM|、|MN|、|PN|成等比数列,可得|MN|2=|PM||PN|.
∴2(x1-x 2)2=
| (x1+2)2+(x2-2 +4)2 |
| (x2+2)2+(x2-2 +4)2 |
| 2 |
| 2 |
即 (x1+x 2)2-4x1•x2=|x1•x2+2(x1+x2)+4|,∴(4+2a)2-16=|4+2(4+2a)+4|,
解得 a=1,
故答案为 1.
点评:本题主要考查把参数方程化为普通方程的方法,把极坐标方程化为直角坐标方程的方法,直线和抛物线的位置关系的应用,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
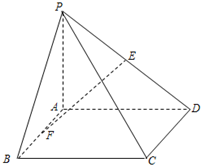 (2012•武昌区模拟)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,AB=
(2012•武昌区模拟)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,AB= (2012•武昌区模拟)2011年武汉电视台问政直播节日首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
(2012•武昌区模拟)2011年武汉电视台问政直播节日首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示: