题目内容
在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足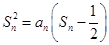 .
.
(1)求Sn的表达式;
(2)设bn=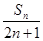 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
【答案】
(1)因为 ,所以n≥2,sn2=(sn-sn-1)(sn-
,所以n≥2,sn2=(sn-sn-1)(sn-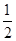 ),
),
所以sn=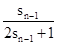 ,即
,即 =2(n≥2)
=2(n≥2)
所以, =2n-1
=2n-1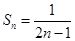 ,
,
(2) 由(1)得,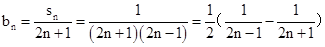
所以,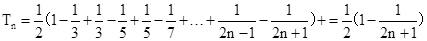 ,
,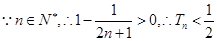
又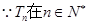 是增函数,
是增函数,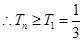 ,故结论得证.
,故结论得证.
【解析】
试题分析:(1)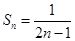 ,(2)
,(2)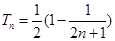
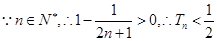
又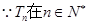 是增函数,
是增函数,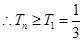 ,故结论得证.
,故结论得证.
考点:本题主要考查数列的前n项和与通项的关系,“裂项相消法”,不等式的证明。
点评:中档题,本题综合考查数列的前n项和与通项的关系,“裂项相消法”,不等式的证明。涉及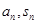 ,往往通过研究
,往往通过研究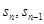 的差,确定数列的通项公式。“裂项相消法”“分组求和法”“错位相减法”是常常考查的数列求和方法。
的差,确定数列的通项公式。“裂项相消法”“分组求和法”“错位相减法”是常常考查的数列求和方法。

练习册系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.