Question

已知数列{a_n}各项均为正数，观察下面的程序框图
（1）若d≠0，分别写出当k=2，k=3时s的表达式．
（2）当输入a₁=d=2，k=100 时，求s的值（ 其中2的高次方不用算出）．

Answer 1

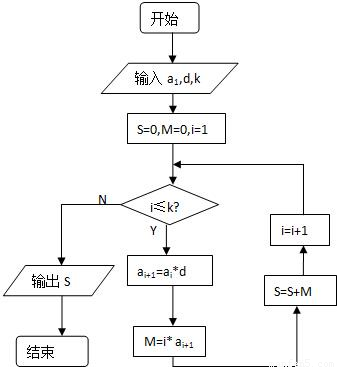
【答案】分析：（1）经过分析，程序框图为当型循环结构，按照框图题意分析求出{a_n}的前n项和即可．
（2）根据（1）的结论，得到a₁d+2a₁d²+3a₁d³+…+100a₁d¹⁰⁰，然后错位相减法求a₁d+2a₁d²+3a₁d³+…+100a₁d¹⁰⁰的和即得．
解答：解：（1）当k=2时   s=a₁d+2a₁d²
当k=3 时   s=a₁d+2a₁d²+3a₁d³
（2）∵s=a₁d+2a₁d²+3a₁d³+…+100a₁d¹⁰⁰
=2²+2×2³+3×2⁴+4×2⁵+…+100×2¹⁰¹
∴2×s=2³+2×2⁴+3×2⁵+4×2⁶+…+100×2¹⁰¹
∴-s=2²+2³+2⁴+2⁵+…+2¹⁰¹-100×2¹⁰²
∴-s=2¹⁰²-4-100×2¹⁰²
∴s=99×2¹⁰²+4
点评：本题考查程序框图，数列的概念及简单表示方法，数列的求和，通过对知识的熟练把握，分别进行求值，属于基础题．