题目内容
如图半径为2的圆内接等腰梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
(1)写出这个梯形周长y和腰长x间的函数式,并求出它的定义域;
(2)求出周长y的最大值及相应x的值.

(1)写出这个梯形周长y和腰长x间的函数式,并求出它的定义域;
(2)求出周长y的最大值及相应x的值.

(1)如图所示,过点C作CE⊥AB,垂足为E,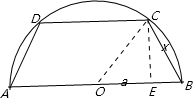
设OE=a,则EB=2-a,∴OC2-OE2=BC2-BE2,即22-a2=x2-(2-a)2,∴a=
;
∴y=AB+2BC+CD=4+2x+2a=4+2x+
=-
+2x+8;由0<a<2,得0<
<2,∴0<x<2
;
所以,周长y=-
+2x+8x∈(0,2
);
(2)周长函数y=-
+2x+8=-
(x-2)2+10,其中x∈(0,2
),所以,当x=2时,y有最大值,为10.

设OE=a,则EB=2-a,∴OC2-OE2=BC2-BE2,即22-a2=x2-(2-a)2,∴a=
| 8-x2 |
| 4 |
∴y=AB+2BC+CD=4+2x+2a=4+2x+
| 8-x2 |
| 2 |
| x2 |
| 2 |
| 8-x2 |
| 4 |
| 2 |
所以,周长y=-
| x2 |
| 2 |
| 2 |
(2)周长函数y=-
| x2 |
| 2 |
| 1 |
| 2 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为正数,
为正数, ,且
,且 ,求证:
,求证: .
.
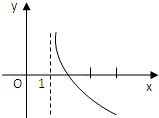

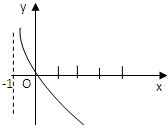
 ,则( )
,则( )