题目内容
(12分)直线l的方程为(a+1)x+y+2-a=0 (a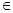 R)。
R)。
(1)若l在两坐标轴上的截距相等,求a的值;
(2)若l不经过第二象限,求实数a的取值范围。
【答案】
直线不过原点时, 或
或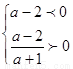
(1)a值为0或2;(2)a≤-1。
【解析】本题主要考查直线方程的一般式,直线在坐标轴上的截距的定义,直线在坐标系中的位置与它的斜率、截距的关系,属于基础题
(Ⅰ)根据直线方程求出它在两坐标轴上的截距,根据它在两坐标轴上的截距相等,求出a的值,即得直线l方程.
(Ⅱ)把直线方程化为斜截式为 y=-(a+1)x-a-2,若l不经过第二象限,则a=-1 或 -(a+1)>0,-a-2≤0 ,由此求得实数a的取值范围
解:(1)当直线l过原点时,该直线在x轴和y轴上的截距为零。
∴a=2,方程为3x+y=0
若a≠2,则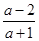 =a-2,a+1=1,a=0
=a-2,a+1=1,a=0
此时方程为x+y+2=0
∴所求a值为0或2
(2)∵直线过原点时,y=-3x经过第二象限,不合题意
|
|
|
 或
或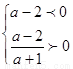
∴a≤-1

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目