题目内容
设直线l的方程为(a+1)x+y+2-a=0(a∈R),若直线l不经过第二象限,则实数a的取值范围
(-∞,-1]
(-∞,-1]
.分析:化直线的一般式方程为斜截式方程,求出直线的斜率,再由直线系方程求出直线恒过定点,结合图形可知,要使直线l不经过第二象限,则斜率大于等于0,由斜率大于等于0求解a的取值范围.
解答: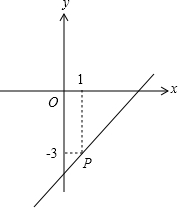 解:由直线l:(a+1)x+y+2-a=0,得x+y+2+a(x-1)=0.
解:由直线l:(a+1)x+y+2-a=0,得x+y+2+a(x-1)=0.
联立
,解得
.
∴直线l:(a+1)x+y+2-a=0恒过定点P(1,-3).
如图,
∵直线l的斜率为-(a+1),要使直线l不经过第二象限,
则-(a+1)≥0,解得a≤-1.
∴实数a的取值范围是(-∞,-1].
故答案为:(-∞,-1].
 解:由直线l:(a+1)x+y+2-a=0,得x+y+2+a(x-1)=0.
解:由直线l:(a+1)x+y+2-a=0,得x+y+2+a(x-1)=0.联立
|
|
∴直线l:(a+1)x+y+2-a=0恒过定点P(1,-3).
如图,
∵直线l的斜率为-(a+1),要使直线l不经过第二象限,
则-(a+1)≥0,解得a≤-1.
∴实数a的取值范围是(-∞,-1].
故答案为:(-∞,-1].
点评:本题考查了确定直线位置关系的集合要素,若直线的斜率一定且直线过定点,则直线在平面中的位置确定,是基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目