ЬтФПФкШн
ЁОЬтФПЁП2008Фъ5дТ12Ше14ЪБ28Зж04УыЃЌЫФДЈЪЁАЂАгВизхЧМзхзджЮжнуыДЈЯиЗЂЩњРяЪЯ8.0МЖЕие№ЃЌЕие№дьГЩ69227ШЫгіФбЃЌ374643ШЫЪмЩЫЃЌ17923ШЫЪЇзйЃЎжиЧьжкЖрвНЮёЙЄзїепКЭжОдИепМгШыСЫПЙджОШдЎааЖЏЃЎЦфжажиЧьШ§ЯПжааФвНдКЭтПЦХЩГігЩ5УћЙЧИЩвНЩњзщГЩЕФОШдЎаЁзщЃЌБМИАЪмджЕквЛЯпВЮгыОШдЎЃЎЯжНЋет5УћвНЩњЗжБ№ЫцЛњЗжХфЕНЪмджзюбЯжиЕФуыДЈЯиЁЂББДЈЯиЁЂУржёШ§ЯижаЕФФГвЛИіЃЎ
ЃЈ1ЃЉЧѓУПИіЯижСЩйЗжХфЕНвЛУћвНЩњЕФИХТЪЃЎ
ЃЈ2ЃЉШєНЋЫцЛњЗжХфЕНуыДЈЯиЕФШЫЪ§МЧЮЊІЮЃЌЧѓЫцЛњБфСПІЮЕФЗжВМСаЃЌЦкЭћКЭЗНВюЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКP= 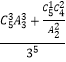 =
= ![]()
ЃЈ2ЃЉНтЃКгЩЬѕМўПЩжЊЃЌІЮЁЋBЃЈ5ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЙЪPЃЈІЮ=iЃЉ= ![]()
![]() ЃЌЃЈi=0ЃЌ1ЃЌ2ЃЌЁЃЌ5ЃЉЃЌ
ЃЌЃЈi=0ЃЌ1ЃЌ2ЃЌЁЃЌ5ЃЉЃЌ
ЙЪІЮЕФЗжВМСаЮЊЃК
ІЮ | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
ЁрEЃЈІЮЃЉ=np=5ЁС ![]() =
= ![]() ЃЌ
ЃЌ
DЃЈІЮЃЉ=npЃЈ1ЉpЃЉ=5ЁС ![]() ЁС
ЁС ![]() =
= ![]()
ЁОНтЮіЁПЃЈ1ЃЉ5УћвНЩњЗж3зщЙВга2ЃЌ2ЃЌ1КЭ1ЃЌ1ЃЌ3СНжжЗжЗЈЃЌШЛКѓдйНЋШ§зщЫцЛњЗжЕНШ§ИіЯиЙВга ![]() +
+ ![]()
![]()
![]() жжАВХХЗНЗЈЃЛШє5УћвНЩњЫцЛњАВХХЙВ35жжАВХХЗНЗЈЃЌИљОнЙХЕфИХаЭИХТЪЙЋЪНПЩЧѓЕУЫљЧѓИХТЪЃЛЃЈ2ЃЉУПУћвНЩњБЛЗжЕНуыДЈЯиЕФИХТЪЖМЯрЕШЖМЕШгк
жжАВХХЗНЗЈЃЛШє5УћвНЩњЫцЛњАВХХЙВ35жжАВХХЗНЗЈЃЌИљОнЙХЕфИХаЭИХТЪЙЋЪНПЩЧѓЕУЫљЧѓИХТЪЃЛЃЈ2ЃЉУПУћвНЩњБЛЗжЕНуыДЈЯиЕФИХТЪЖМЯрЕШЖМЕШгк ![]() ЃЌЫљвдЗжХфЕНуыДЈЕФвНЩњШЫЪ§ІЮЗўДгЖўЯюЗжВМЃЌИљОнЖўЯюЗжВМИХТЪЙЋЪНПЩЧѓЦфЗжВМСаМАЦкЭћКЭЗНВюЃЎ
ЃЌЫљвдЗжХфЕНуыДЈЕФвНЩњШЫЪ§ІЮЗўДгЖўЯюЗжВМЃЌИљОнЖўЯюЗжВМИХТЪЙЋЪНПЩЧѓЦфЗжВМСаМАЦкЭћКЭЗНВюЃЎ
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫРыЩЂаЭЫцЛњБфСПМАЦфЗжВМСаЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮедкЩфЛїЁЂВњЦЗМьбщЕШР§згжаЃЌЖдгкЫцЛњБфСПXПЩФмШЁЕФжЕЃЌЮвУЧПЩвдАДвЛЖЈДЮађвЛвЛСаГіЃЌетбљЕФЫцЛњБфСПНазіРыЩЂаЭЫцЛњБфСПЃЎРыЩЂаЭЫцЛњБфСПЕФЗжВМСаЃКвЛАуЕФ,ЩшРыЩЂаЭЫцЛњБфСПXПЩФмШЁЕФжЕЮЊx1,x2,.....,xi,......,xnЃЌXШЁУПвЛИіжЕ xi(i=1,2,......ЃЉЕФИХТЪP(ІЮ=xiЃЉЃНPiЃЌдђГЦБэЮЊРыЩЂаЭЫцЛњБфСПX ЕФИХТЪЗжВМЃЌМђГЦЗжВМСаВХФме§ШЗНтД№ДЫЬтЃЎ

 ШЋФмВтПивЛБОКУОэЯЕСаД№АИ
ШЋФмВтПивЛБОКУОэЯЕСаД№АИЁОЬтФПЁПФГЭЌбЇгУЁАЮхЕуЗЈЁБЛКЏЪ§fЃЈxЃЉ=AsinЃЈІиx+![]() ЃЉЃЈІиЃО0ЃЌ|
ЃЉЃЈІиЃО0ЃЌ|![]() |ЃМ
|ЃМ![]() ЃЉдкФГвЛИіжмЦкФкЕФЭМЯѓЪБЃЌСаБэВЂЬюШыСЫВПЗжЪ§ОнЃЌШчБэЃК
ЃЉдкФГвЛИіжмЦкФкЕФЭМЯѓЪБЃЌСаБэВЂЬюШыСЫВПЗжЪ§ОнЃЌШчБэЃК
Іиx+Іе | 0 |
| Іа |
| 2Іа |
x |
|
| |||
Asin(Іиx+ІеЃЉ | 0 | 2 | -2 | 0 |
ЃЈ1ЃЉЧыНЋЩЯБэЪ§ОнВЙГфЭъећЃЌЬюаДдкД№ЬтОэЩЯЯргІЮЛжУЃЌВЂжБНгаДГіКЏЪ§fЃЈxЃЉЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєfЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌЧѓcosЃЈ2ІС+
ЃЌЧѓcosЃЈ2ІС+![]() ЃЉЕФжЕЃЎ
ЃЉЕФжЕЃЎ