题目内容
已知函数f(x)=ax_3+bx2+(b-a)x(a,b是不同时为零的常数),其导函数为f′(x).(1)当a=
 时,若不等式f'(x)>-
时,若不等式f'(x)>- 对任意x∈R恒成立,求b的取值范围;
对任意x∈R恒成立,求b的取值范围;(2)若函数f(x)为奇函数,且在x=1处的切线垂直于直线x+2y-3=0,讨论关于x的方程f(x)=k在[-1,+∞)上实数根的情况.
【答案】分析:(1)求导函数,利用不等式f'(x)>- 对任意x∈R恒成立,可得x2+2bx+b>0恒成立,利用判别式可得b的取值范围;
对任意x∈R恒成立,可得x2+2bx+b>0恒成立,利用判别式可得b的取值范围;
(2)利用函数f(x)为奇函数,函数f(x)在x=1处的切线垂直于直线x+2y-3=0,求出函数解析式,从而确定函数的单调性,求出函数的极值,再分类讨论,即可得到结论.
解答:解:(1)当a= 时,f′(x)=x2+2bx+b-
时,f′(x)=x2+2bx+b- ,
,
依题意f′(x)=x2+2bx+b- >
> ,即x2+2bx+b>0恒成立
,即x2+2bx+b>0恒成立
∴△=4b2-4b<0,解得0<b<1
所以b的取值范围是(0,1);
(2)∵函数f(x)为奇函数,∴f(-x)=-f(x),∴b=0,∴函数f(x)=ax3-ax
∴f′(x)=3ax2-a
∵函数f(x)在x=1处的切线垂直于直线x+2y-3=0
∴a=1
∴f(x)=x3-x,f′(x)=3x2-1
∴f(x)在(-∞,-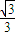 ),(
),(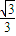 ,+∞)上单调递增,在(-
,+∞)上单调递增,在(- ,
,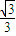 )上单调递减
)上单调递减
由f(x)=0得x=±1,x=0
f(x)在[-1,+∞)上图象如图所示
∵f( )=
)= ,f(
,f( )=-
)=- ,
,
∴当k<-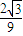 时,f(x)=k在[-1,+∞)上没有实数根;
时,f(x)=k在[-1,+∞)上没有实数根;
当k>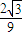 或k=-
或k=- 时,f(x)=k在[-1,+∞)上有且只有一个实数根;
时,f(x)=k在[-1,+∞)上有且只有一个实数根;
当k=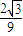 或-
或-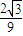 <k<0时,f(x)=k在[-1,+∞)上有两个实数根;
<k<0时,f(x)=k在[-1,+∞)上有两个实数根;
当0<k< 时,f(x)=k在[-1,+∞)上有三个实数根.
时,f(x)=k在[-1,+∞)上有三个实数根.
点评:本题考查导数知识的运用,考查函数的单调性与极值,考查分类讨论的数学思想,考查方程根的讨论,属于中档题.
 对任意x∈R恒成立,可得x2+2bx+b>0恒成立,利用判别式可得b的取值范围;
对任意x∈R恒成立,可得x2+2bx+b>0恒成立,利用判别式可得b的取值范围;(2)利用函数f(x)为奇函数,函数f(x)在x=1处的切线垂直于直线x+2y-3=0,求出函数解析式,从而确定函数的单调性,求出函数的极值,再分类讨论,即可得到结论.
解答:解:(1)当a=
 时,f′(x)=x2+2bx+b-
时,f′(x)=x2+2bx+b- ,
,依题意f′(x)=x2+2bx+b-
 >
> ,即x2+2bx+b>0恒成立
,即x2+2bx+b>0恒成立∴△=4b2-4b<0,解得0<b<1
所以b的取值范围是(0,1);
(2)∵函数f(x)为奇函数,∴f(-x)=-f(x),∴b=0,∴函数f(x)=ax3-ax
∴f′(x)=3ax2-a
∵函数f(x)在x=1处的切线垂直于直线x+2y-3=0
∴a=1
∴f(x)=x3-x,f′(x)=3x2-1
∴f(x)在(-∞,-
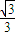 ),(
),(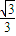 ,+∞)上单调递增,在(-
,+∞)上单调递增,在(- ,
,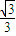 )上单调递减
)上单调递减由f(x)=0得x=±1,x=0
f(x)在[-1,+∞)上图象如图所示

∵f(
 )=
)= ,f(
,f( )=-
)=- ,
,∴当k<-
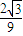 时,f(x)=k在[-1,+∞)上没有实数根;
时,f(x)=k在[-1,+∞)上没有实数根;当k>
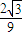 或k=-
或k=- 时,f(x)=k在[-1,+∞)上有且只有一个实数根;
时,f(x)=k在[-1,+∞)上有且只有一个实数根;当k=
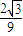 或-
或-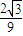 <k<0时,f(x)=k在[-1,+∞)上有两个实数根;
<k<0时,f(x)=k在[-1,+∞)上有两个实数根;当0<k<
 时,f(x)=k在[-1,+∞)上有三个实数根.
时,f(x)=k在[-1,+∞)上有三个实数根.点评:本题考查导数知识的运用,考查函数的单调性与极值,考查分类讨论的数学思想,考查方程根的讨论,属于中档题.

练习册系列答案
相关题目