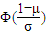题目内容
以Φ（x）表示标准正态总体在区间（-∞，x）内取值的概率，若随机变量ξ服从正态分布N（μ，σ2），则概率P（|ξ-μ|＜σ）等于（ ）
| A．Φ（μ+σ）-Φ（μ-σ） | B．Φ（1）-Φ（-1） | C．Φ(
| D．2Φ（μ+σ） |
考查N（μ，σ2）与N（0，1）的关系：
若ξ～N（μ，σ2），
则P(x1＜x＜x2)=Φ(
)-Φ(
)
P（|ξ-μ|＜σ）
=P（μ-σ＜ξ＜μ+σ）
=Φ(
)-Φ(
)
=Φ（1）-Φ（-1）
故选B．
若ξ～N（μ，σ2），
则P(x1＜x＜x2)=Φ(
| x2-μ |
| σ |
| x1-μ |
| σ |
P（|ξ-μ|＜σ）
=P（μ-σ＜ξ＜μ+σ）
=Φ(
| μ+σ-μ |
| σ |
| μ-σ-μ |
| σ |
=Φ（1）-Φ（-1）
故选B．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
以Φ（x）表示标准正态总体在区间（-∞，x）内取值的概率，若随机变量ξ服从正态分布N（μ，σ2），则概率P（|ξ-μ|＜σ）等于（ ）
| A、Φ（μ+σ）-Φ（μ-σ） | ||
| B、Φ（1）-Φ（-1） | ||
C、Φ(
| ||
| D、2Φ（μ+σ） |
