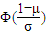题目内容
11、以Φ（x）表示标准正态总体在区间（-∞，x）内取值的概率，设随机变量ξ服从标准正态分布N（0，1），已知Φ（-1.96）=0.026，则P（|ξ|＜1.96）=
0.948
．分析：解法一：根据变量符合正态分布，且对称轴是x=0，得到P（|ξ|＜1.96）=P（-1.96＜ξ＜1.96），应用所给的Φ（-1.96）=0.025，条件得到结果，
解法二：本题也可以这样解根据曲线的对称轴是直线x=0，得到一系列对称关系，代入条件得到结果．
解法二：本题也可以这样解根据曲线的对称轴是直线x=0，得到一系列对称关系，代入条件得到结果．
解答：解：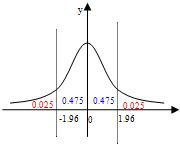
解法一：∵ξ～N（0，1）
∴P（|ξ|＜1.96）
=P（-1.96＜ξ＜1.96）
=Φ（1.96）-Φ（-1.96）
=1-2Φ（-1.96）
=0.950
解法二：因为曲线的对称轴是直线x=0，
所以由图知P（ξ＞1.96）=P（ξ≤-1.96）=Φ（-1.96）=0.026
∴P（|ξ|＜1.96）=1-0.26-0.26=0.948
故答案为：0.948．
解法一：∵ξ～N（0，1）∴P（|ξ|＜1.96）
=P（-1.96＜ξ＜1.96）
=Φ（1.96）-Φ（-1.96）
=1-2Φ（-1.96）
=0.950
解法二：因为曲线的对称轴是直线x=0，
所以由图知P（ξ＞1.96）=P（ξ≤-1.96）=Φ（-1.96）=0.026
∴P（|ξ|＜1.96）=1-0.26-0.26=0.948
故答案为：0.948．
点评：本题考查正态曲线的特点及曲线所表示的意义，主要考查对称性，是一个数形结合的问题，是一个遇到一定要得分数的题目．
练习册系列答案
相关题目
以Φ（x）表示标准正态总体在区间（-∞，x）内取值的概率，若随机变量ξ服从正态分布N（μ，σ2），则概率P（|ξ-μ|＜σ）等于（ ）
| A、Φ（μ+σ）-Φ（μ-σ） | ||
| B、Φ（1）-Φ（-1） | ||
C、Φ(
| ||
| D、2Φ（μ+σ） |
