题目内容
(2013•德州一模)直线y=-
x+m与圆x2+y2=1在第一象限内有两个不同的交点,则m取值范围是( )
| ||
| 3 |
分析:求出直线过(0,1)时m的值,以及直线与圆相切时m的值,即可确定出满足题意m的范围.
解答: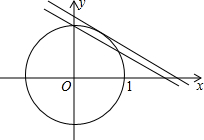 解:如图所示:
解:如图所示:
当直线过(0,1)时,将(0,1)代入直线方程得:m=1;
当直线与圆相切时,圆心到切线的距离d=r,即
=1,
解得:m=
或m=-
(舍去),
则直线与圆在第一象限内有两个不同的交点时,m的范围为1<m<
.
故选D
 解:如图所示:
解:如图所示:当直线过(0,1)时,将(0,1)代入直线方程得:m=1;
当直线与圆相切时,圆心到切线的距离d=r,即
| |m| | ||||||
|
解得:m=
2
| ||
| 3 |
2
| ||
| 3 |
则直线与圆在第一象限内有两个不同的交点时,m的范围为1<m<
2
| ||
| 3 |
故选D
点评:此题考查了直线与圆相交的性质,利用了数形结合的思想,熟练掌握数形结合法是解本题的关键.

练习册系列答案
相关题目