题目内容
(本小题满分12分)
已知函数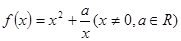
(1)判断函数 的奇偶性;
的奇偶性;
(2)若 在区间
在区间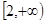 是增函数,求实数
是增函数,求实数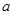 的取值范围。
的取值范围。
【答案】
(1)当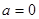 时,
时,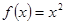 为偶函数;当
为偶函数;当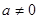 时,
时,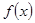 既不是奇函数也不是偶函数.
既不是奇函数也不是偶函数.
(2)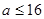
【解析】
试题分析:(1)当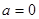 时,
时,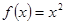 为偶函数;当
为偶函数;当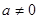 时,
时,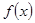 既不是奇函数也不是偶函数.
既不是奇函数也不是偶函数.
(2)设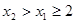 ,
,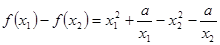
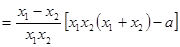 ,
,
由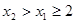 得
得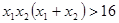 ,
,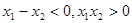
要使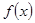 在区间
在区间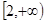 是增函数只需
是增函数只需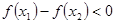 ,
,
即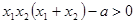 恒成立,则
恒成立,则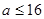 。
。
另解(导数法):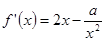 ,要使
,要使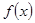 在区间
在区间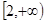 是增函数,只需当
是增函数,只需当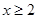 时,
时,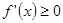 恒成立,即
恒成立,即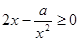 ,则
,则 恒成立,
恒成立,
故当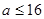 时,
时,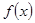 在区间
在区间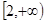 是增函数。
是增函数。
考点:函数的单调性与导数的关系;函数奇偶性的判断.
点评: 此题考查函数的单调性与导数的关系,若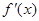 大于0,则
大于0,则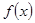 为增函数;若
为增函数;若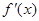 小于0,则
小于0,则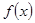 为减函数.
为减函数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目