题目内容
已知函数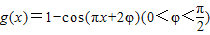 的图象过点
的图象过点 ,若有4个不同的正数xi满足g(xi)=M(0<M<1),且xi<4(i=1,2,3,4),则x1+x2+x3+x4等于 .
,若有4个不同的正数xi满足g(xi)=M(0<M<1),且xi<4(i=1,2,3,4),则x1+x2+x3+x4等于 .
【答案】分析:先由g(x)过点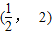 ,求得φ,进而求得函数g(x),再由g(x)=M 在两个周期之内有四个解,则在在一个周期内必有两个解,表示出四个解来相加可得.
,求得φ,进而求得函数g(x),再由g(x)=M 在两个周期之内有四个解,则在在一个周期内必有两个解,表示出四个解来相加可得.
解答:解:∵g(x)过点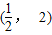 ,
,
∴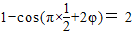
即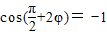
即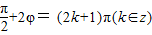
又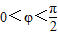
∴φ=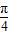
∴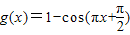
∵g(x)=M 在两个周期之内有四个解,
∴在一个周期内有两个解
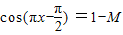

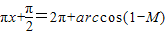
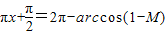
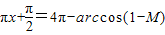
以上四式相加得:
x1+x2+x3+x4=6
故答案为:6
点评:本题主要考查三角函数的周期性及三角方程有多解的特性,但都有相应的规律,与周期有关.
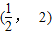 ,求得φ,进而求得函数g(x),再由g(x)=M 在两个周期之内有四个解,则在在一个周期内必有两个解,表示出四个解来相加可得.
,求得φ,进而求得函数g(x),再由g(x)=M 在两个周期之内有四个解,则在在一个周期内必有两个解,表示出四个解来相加可得.解答:解:∵g(x)过点
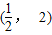 ,
,∴
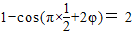
即
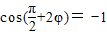
即
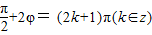
又
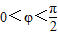
∴φ=
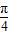
∴
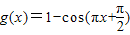
∵g(x)=M 在两个周期之内有四个解,
∴在一个周期内有两个解
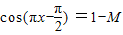

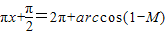
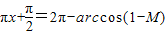
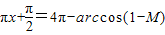
以上四式相加得:
x1+x2+x3+x4=6
故答案为:6
点评:本题主要考查三角函数的周期性及三角方程有多解的特性,但都有相应的规律,与周期有关.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 的图象过点A(3,7),则此函的最小值是 .
的图象过点A(3,7),则此函的最小值是 . 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
. 的解析式;
的解析式; ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值; 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围. 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数