Question

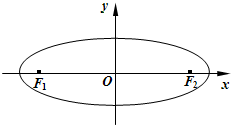已知椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）上任意一点到两焦点距离之和为2

3

，离心率为

3

3

，左、右焦点分别为F₁，F₂，点P是右准线上任意一点，过F₂作直线PF₂的垂线F₂Q交椭圆于Q点．
（1）求椭圆E的标准方程；
（2）证明：直线PQ与直线OQ的斜率之积是定值；
（3）点P的纵坐标为3，过P作动直线l与椭圆交于两个不同点M、N，在线段MN上取点H，满足

MP

PN

=

MH

HN

，试证明点H恒在一定直线上．

Answer 1

分析：（1）由题意可得

2a=2 3 e= c a = 3 3 a2=b2+c2

，解出即可；
（2）由（1）可知：椭圆的右准线方程为x=

a2

c

=3，设P（3，y₀），Q（x₁，y₁），由PF₂⊥F₂Q，可得kQF2•kPF2=-1，利用斜率计算公式可得k_PQ•k_OQ及

y

2 1

=2(1-

x 2 1

3

)代入化简得直线PQ与直线OQ的斜率之积是定值．
（3）设过P（3，3）的直线l与椭圆交于两个不同点M（x₁，y₁），N（x₂，y₂），点H（x，y），由点M，N在椭圆上可得2

x

2 1

+3

y

2 1

=6，2

x

2 2

+3

y

2 2

=6．
设

MP

PN

=

MH

HN

=λ，则

MP

=-λ

PN

，

MH

=λ

NH

，可得（3-x₁，3-y₁）=-λ（x₂-3，y₂-3），（x-x₁，y-y₁）=λ（x₂-x，y₂-y），即可证明6x+9y为定值．

解答：解：（1）由题意可得

2a=2 3 e= c a = 3 3 a2=b2+c2

，解得a=

3

，c=1，b=

2

所以椭圆E：

x2

3

+

y2

2

=1．
（2）由（1）可知：椭圆的右准线方程为x=

a2

c

=3，
设P（3，y₀），Q（x₁，y₁），
因为PF₂⊥F₂Q，所以kQF2kPF2=

y0

2

•

y1

x1-1

=

y0y1

2(x1-1)

=-1，
所以-y₁y₀=2（x₁-1）
又因为kPQ•kOQ=

y1

x1

•

y1-y0

x1-3

=

y 2 1 -y1y0

x 2 1 -3x1

且

y

2 1

=2(1-

x 2 1

3

)代入化简得kPQ•kOQ=-

2

3

．
即直线PQ与直线OQ的斜率之积是定值-

2

3

．
（3）设过P（3，3）的直线l与椭圆交于两个不同点M（x₁，y₁），N（x₂，y₂），点H（x，y），
则2

x

2 1

+3

y

2 1

=6，2

x

2 2

+3

y

2 2

=6．
设

MP

PN

=

MH

HN

=λ，则

MP

=-λ

PN

，

MH

=λ

NH

，
∴（3-x₁，3-y₁）=-λ（x₂-3，y₂-3），（x-x₁，y-y₁）=λ（x₂-x，y₂-y）
整理得3=

x1-λx2

1-λ

，x=

x1+λx2

1+λ

，3=

y1-λy2

1-λ

，y=

y1+λy2

1+λ

，
∴从而3x=

x 2 1 -λ2 x 2 2

1-λ2

，3y=

y 2 1 -λ2 y 2 2

1-λ2

，
由于2

x

2 1

+3

y

2 1

=6，2

x

2 2

+3

y

2 2

=6，∴我们知道

x

2 1

与

y

2 1

的系数之比为2：3，

x

2 2

与

y

2 2

的系数之比为2：3．
∴6x+9y=

2 x 2 1 -2λ2 x 2 2 +3 y 2 1 -3λ2 y 2 2

1-λ2

=

2 x 2 1 +3 y 2 1 -λ2(2 x 2 2 +3 y 2 2 )

1-λ2

=6，
所以点H恒在直线2x+3y-2=0上．

点评：本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量运算、斜率计算公式等基础知识与基本技能，考查了分析问题和解决问题的能力、推理能力和计算能力．