题目内容
在数列{an}中,a1=1,an+1=1-(1)求证:数列{bn}是等差数列.
(2)求证:在数列{an}中对于任意的N∈N*都有an+1<an.
(3)设cn=![]() ,试问数列{cn}中是否存在三项它们可以构成等差数列?如果存在,求出这三项;如果不存在,请说明理由.
,试问数列{cn}中是否存在三项它们可以构成等差数列?如果存在,求出这三项;如果不存在,请说明理由.
(1)证明:因为bn+1-bn=![]() -
-![]() ?
?
=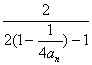 -
-![]() =
=![]() -
-![]() =2(n∈N*),?
=2(n∈N*),?
所以数列{bn}是等差数列. ?
(2)证明:因为a1=1,所以b1=![]() =2.?所以bn=2+(n-1)×2=2n.?
=2.?所以bn=2+(n-1)×2=2n.?
由bn=![]() ,得2an-1=
,得2an-1=![]() =
=![]() (n∈N*),?所以an=
(n∈N*),?所以an=![]() . ?
. ?
所以an+1-an=![]() -
-![]() =
=![]() <0.?
<0.?
所以在数列{an}中对于任意的n∈N*都有an+1<an. ?
(3)解:cn=(![]() )bn=2n,?
)bn=2n,?
设{cn}中存在三项cm,cn,cP(m<n<P,m,n,P∈N*)成等差数列,?
则2·2n=
2n-m+1=1+2P-m. ?
因为m<n<P,m,n,P∈N*,所以n-m+1,P-m∈N*.?
2n-m+1为偶数,1+2P-m为奇数,?所以2n-m+1与1+2P-m不可能相等. ?
所以数列{cn}中不存在可以构成等差数列的三项.

 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.