题目内容
 给定两个长度为1的平面向量
给定两个长度为1的平面向量| OA |
| OB |
(1)求|
| OA |
| OB |
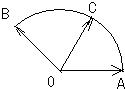
(2)如图所示,点C在以O为圆心的圆弧
 |
| AB |
| OC |
| OA |
| OB |
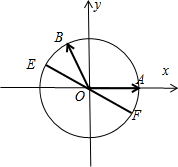
(3)若点E、点F在以O为圆心,1为半径的圆上,且
| OE |
| FO |
| BE |
| AF |
| BE |
| AF |
分析:(1)直接利用向量的模的运算法则,求出|
+
|;
(2)建立坐标系如图,推出A,B,C的坐标,利用
=x
+y
,求出x,y通过三角函数求出x+y的最大值.
(3)设出E,F,直接利用
•
计算,求出最大值,推出向量的夹角的大小即可.
| OA |
| OB |
(2)建立坐标系如图,推出A,B,C的坐标,利用
| OC |
| OA |
| OB |
(3)设出E,F,直接利用
| BE |
| AF |
解答:解:(1)|
+
|;
=
=
=1 (5分)
(2)如图所示,建立直角坐标系,则A(1,0),B(-
,
),C(cosθ,sinθ).
由
=x
+y
,得cosθ=x-
,sinθ=
.
即x=cosθ+
sinθ , y=
sinθ.则x+y=
sinθ+cosθ=2sin(θ+
)
又θ∈[0,
],则θ+
∈[
,
],故当θ=
时,x+y的最大值是2.…(11分)
(3)点E、点F在以O为圆心,1为半径的圆上,且
=
设F(cosα,sinα),E(-cosα,-sinα),
•
=(-cosα+
,-sinα-
)(cosα-1,sinα)=
cos(α+
)-
,
所以
•
的最大值为为
-
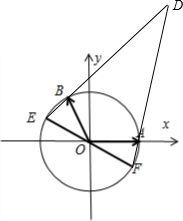
.此时如图∠E=∠F=75°,∠EDF=30°,
即θ=
时,
•
的最大值为
-
.(16分).
| OA |
| OB |
(
|
|
=
1+2×1×1×(-
|
(2)如图所示,建立直角坐标系,则A(1,0),B(-
| 1 |
| 2 |
| ||
| 2 |


由
| OC |
| OA |
| OB |
| y |
| 2 |
| ||
| 2 |
即x=cosθ+
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| π |
| 6 |
又θ∈[0,
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
(3)点E、点F在以O为圆心,1为半径的圆上,且
| OE |
| FO |
设F(cosα,sinα),E(-cosα,-sinα),
| BE |
| AF |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
| 3 |
| 2 |
所以
| BE |
| AF |
| 3 |
| 3 |
| 2 |
即θ=
| π |
| 6 |
| BE |
| AF |
| 3 |
| 3 |
| 2 |
点评:本题是综合题,考查向量的基本运算,向量的数量积,三角函数的有关计算,考查计算能力,作图能力.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 给定两个长度为1的平面向量
给定两个长度为1的平面向量 给定两个长度为1的平面向量
给定两个长度为1的平面向量 给定两个长度为1的平面向量
给定两个长度为1的平面向量 给定两个长度为1的平面向量
给定两个长度为1的平面向量 如图,给定两个长度为1的平面向量
如图,给定两个长度为1的平面向量