题目内容
 给定两个长度为1的平面向量
给定两个长度为1的平面向量| OA |
| OB |
| OC |
| OA |
| OB |
(1)若∠AOC=30°,求x,y的值;
(2)求x+y的最大值.
分析:(1)以O为原点,OA方向为x轴正方向建立坐标系,分别求出A,B的坐标,及∠AOC=30°时,C的坐标,进而根据
=x
+y
,构造关于x,y的方程,解方程即可得到满足条件的x,y的值;
(2)则
=x
+y
=(x,0)+(-
,
y)=(cosα,sinα),我们求出x+y的表达式,然后根据三角函数的性质,即可得到x+y的最大值.
| OC |
| OA |
| OB |
(2)则
| OC |
| OA |
| OB |
| y |
| 2 |
| ||
| 2 |
解答:解:(1)建立如图所示的坐标系,
则A(1,0),B(cos120°,sin120°),即B(-
,
)
即B(-
,
).
设∠AOC=α,则
=(cosα,sinα).
∴当∠AOC=30°时,
=(
,
)
则
∴x=
,y=
…(7分)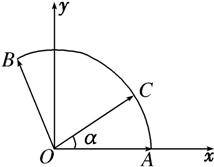
(2)∵
=x
+y
=(x,0)+(-
,
y)=(cosα,sinα).
∴
∴
∴x+y=
sinα+cosα=2sin(α+30°).
∵0°≤α≤120°.∴30°≤α+30°≤150°.
∴x+y有最大值2,当α=60°时取最大值2.…(14分)
则A(1,0),B(cos120°,sin120°),即B(-
| 1 |
| 2 |
| ||
| 2 |
即B(-
| 1 |
| 2 |
| ||
| 2 |
设∠AOC=α,则
| OC |
∴当∠AOC=30°时,
| OC |
| ||
| 2 |
| 1 |
| 2 |
则
|
∴x=
2
| ||
| 3 |
| ||
| 3 |

(2)∵
| OC |
| OA |
| OB |
| y |
| 2 |
| ||
| 2 |
∴
|
∴
|
∴x+y=
| 3 |
∵0°≤α≤120°.∴30°≤α+30°≤150°.
∴x+y有最大值2,当α=60°时取最大值2.…(14分)
点评:本题考查的知识点是平面向量的综合应用,三角函数的性质,其中建立坐标系,分别求出A,B,C点的坐标,将一个几何问题代数化,是解答本题的关键.

练习册系列答案
相关题目
 给定两个长度为1的平面向量
给定两个长度为1的平面向量 给定两个长度为1的平面向量
给定两个长度为1的平面向量 给定两个长度为1的平面向量
给定两个长度为1的平面向量
 如图,给定两个长度为1的平面向量
如图,给定两个长度为1的平面向量