题目内容
设服从二项分布 的随机变量
的随机变量 的期望与方差分别是
的期望与方差分别是 和
和 ,则
,则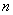 、
、 的值分别是( ).
的值分别是( ).
A. B.
B.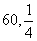 C.
C. D.
D.
【答案】
B
【解析】
试题分析:若随机变量X服从二项分布,即ξ~B(n,p),则随机变量X的期望EX=np,方差DX=np(1-p),由此列方程即可解得n、p的值解:解:由二项分布的性质:EX=np=15,DX=np(1-p)=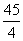 ,解得p=
,解得p= ,n=60,故选 B
,n=60,故选 B
考点:二项分布
点评:本题主要考查了二项分布的性质,二项分布的期望和方差的公式及其用法,离散型随机变量的概率分布的意义,属基础题

练习册系列答案
相关题目
设服从二项分布B~(n,p)的随机变量ξ的期望和方差分别是2.4与1.44,则二项分布的参数n、p的值为( )
| A、n=4,p=0.6 | B、n=6,p=0.4 | C、n=8,p=0.3 | D、n=24,p=0.1 |