题目内容
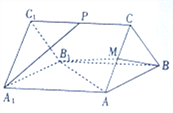
【题目】如图，在三棱柱ABC A1B1C1中，侧棱垂直于底面，AB⊥BC， 
，
E，F分别是A1C1，BC的中点．
(Ⅰ)求证：C1F∥平面ABE；
(Ⅱ)求三棱锥E-ABC的体积．
【答案】(1)详见解析;(2) 
.
【解析】试题分析： （1）证明四边形FGEC1为平行四边形，然后得到C1F∥EG.，即可证出C1F∥平面ABE；
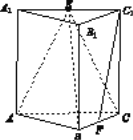
（2）取AC的中点O，连接EO，则EO∥A1A, 所以A1A
平面ABC，利用三棱锥体积公式可求.
试题解析：
(Ⅰ)证明：取AB的中点G，连接EG，FG.
因为E，F，G分别是A1C1，BC，AB的中点，
所以FG∥AC，且FG＝
AC，EC1＝
A1C1.
因为AC∥A1C1，且AC＝A1C1，
所以FG∥EC1，且FG＝EC1，
所以四边形FGEC1为平行四边形，
所以C1F∥EG.
又因为EG平面ABE，C1F平面ABE，
所以C1F∥平面ABE.
(Ⅱ) 取AC的中点O，连接EO，则EO∥A1A, 所以A1A
平面ABC.
.
练习册系列答案
相关题目
