题目内容
给出4个命题:(1)设椭圆长轴长度为2a(a>0),椭圆上的一点P到一个焦点的距离是
 ,P到一条准线的距离是
,P到一条准线的距离是 ,则此椭圆的离心率为
,则此椭圆的离心率为 .
.(2)若椭圆
 (a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|为定值.
(a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|为定值.(3)如果平面内动点M到定直线l的距离与M到定点F的距离之比大于1,那么动点M的轨迹是双曲线.
(4)过抛物线焦点F的直线与抛物线交于A、B两点,若A、B在抛物线准线上的射影分别为A1、B1,则FA1⊥FB1.
其中正确命题的序号依次是 .(把你认为正确的命题序号都填上)
【答案】分析:对于(1):椭圆上的一点P到一个焦点的距离是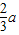 ,P到相应的一条准线的距离是
,P到相应的一条准线的距离是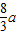 ,则此椭圆的离心率才为
,则此椭圆的离心率才为 .;对于(2)若椭圆
.;对于(2)若椭圆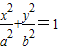 (a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|=4a2为定值;(3)如果平面内动点M到定点F的距离与M到定直线l的距离之比大于1,那么动点M的轨迹才是双曲线;对于(4)由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.
(a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|=4a2为定值;(3)如果平面内动点M到定点F的距离与M到定直线l的距离之比大于1,那么动点M的轨迹才是双曲线;对于(4)由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.
解答: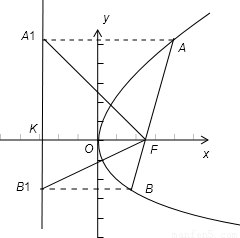 解:对于(1):椭圆上的一点P到一个焦点的距离是
解:对于(1):椭圆上的一点P到一个焦点的距离是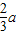 ,P到相应的一条准线的距离是
,P到相应的一条准线的距离是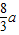 ,则此椭圆的离心率才为
,则此椭圆的离心率才为 .本选项中的准线不一定与焦点对应,故错;
.本选项中的准线不一定与焦点对应,故错;
对于(2)若椭圆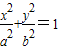 (a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|=4a2为定值,正确.
(a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|=4a2为定值,正确.
(3)如果平面内动点M到定点F的距离与M到定直线l的距离之比大于1,那么动点M的轨迹才是双曲线,故错.
对于(4)如图:设准线与x轴的交点为K,∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,AA1=AF,∴∠AA1F=∠AFA1,又由内错角相等得∠AA1F=∠A1FK,
∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK.
由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,则FA1⊥FB1.正确.
故答案为:(2)(4).
点评:本小题主要考查双曲线的定义、抛物线的定义、以及简单性质的应用、椭圆的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
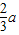 ,P到相应的一条准线的距离是
,P到相应的一条准线的距离是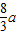 ,则此椭圆的离心率才为
,则此椭圆的离心率才为 .;对于(2)若椭圆
.;对于(2)若椭圆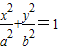 (a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|=4a2为定值;(3)如果平面内动点M到定点F的距离与M到定直线l的距离之比大于1,那么动点M的轨迹才是双曲线;对于(4)由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.
(a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|=4a2为定值;(3)如果平面内动点M到定点F的距离与M到定直线l的距离之比大于1,那么动点M的轨迹才是双曲线;对于(4)由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.解答:
 解:对于(1):椭圆上的一点P到一个焦点的距离是
解:对于(1):椭圆上的一点P到一个焦点的距离是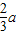 ,P到相应的一条准线的距离是
,P到相应的一条准线的距离是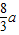 ,则此椭圆的离心率才为
,则此椭圆的离心率才为 .本选项中的准线不一定与焦点对应,故错;
.本选项中的准线不一定与焦点对应,故错;对于(2)若椭圆
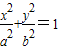 (a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|=4a2为定值,正确.
(a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|=4a2为定值,正确.(3)如果平面内动点M到定点F的距离与M到定直线l的距离之比大于1,那么动点M的轨迹才是双曲线,故错.
对于(4)如图:设准线与x轴的交点为K,∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,AA1=AF,∴∠AA1F=∠AFA1,又由内错角相等得∠AA1F=∠A1FK,
∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK.
由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,则FA1⊥FB1.正确.
故答案为:(2)(4).
点评:本小题主要考查双曲线的定义、抛物线的定义、以及简单性质的应用、椭圆的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
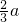 ,P到一条准线的距离是
,P到一条准线的距离是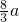 ,则此椭圆的离心率为
,则此椭圆的离心率为 .
. (a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|为定值.
(a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|为定值.