Question

（08年北师大附中月考文）设函数f (x ) = ax³ + bx² + cx + 3－a（a，b，c∈R，且a≠0），当x =－1时，f (x )取得极大值2.

（I）用关于a的代数式分别表示b与c；

（II）当a = 1时，求f (x )的极小值；

（III）求a的取值范围.

Answer 1

解析：（I）= 3ax² + 2bx + c，

由，得：b = a + 1，c = 2－a，

（II）当a = 1时，f (x ) = x³ + 2x² + x + 2，

此时，= 3x² + 4x + 1 = (x + 1)(3x + 1)，

由＞0，得x＜－1或x＞－，＜0，得－1＜x＜－，

故极小值为f (－) =；

（III）由于f (x )在x =－1处有极大值，且a≠0，

∴ x =－1是= 0的实数根，且方程有两个不等实数根，

∴ 另一个根为，

又x =－1处f (x )取得极大值，

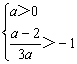∴ 或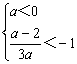，解得：a＞.

故a的取值范围(，+∞).