题目内容
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
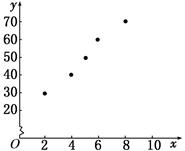
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 .
.
(3)经计算,相关指数 ,你可得到什么结论?
,你可得到什么结论?
(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 .
.(3)经计算,相关指数
 ,你可得到什么结论?
,你可得到什么结论?(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
(1)详见解析;(2)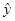 =7x+15;(3)详见解析.
=7x+15;(3)详见解析.
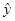 =7x+15;(3)详见解析.
=7x+15;(3)详见解析.试题分析:(1)根据表格中的数据,易得散点图;(2)根据线性回归分析中的相关公式,
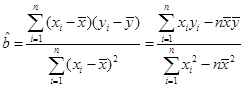 ,
,  ,将表格中的数据代入,即可得到线性回归方程为
,将表格中的数据代入,即可得到线性回归方程为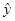 =7x+15;(3)相关指数R2是描述模拟效果好坏的一个量,它的值越接近于1,拟合效果越好,
=7x+15;(3)相关指数R2是描述模拟效果好坏的一个量,它的值越接近于1,拟合效果越好,而对应的残差平方和就越小,在选择模型时,一般选择相关系大的模型,.
(1)根据条件中所给数据易得散点图如下图所示
 4分
4分(2)根据表格中数据,
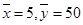 ,
,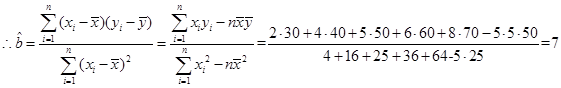 8分
8分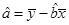 =15, 10分
=15, 10分∴线性回归方程为
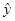 =7x+15. 11分
=7x+15. 11分(3)本题要求学生根据相关指数R2的意义回答问题,结论叙述可以多样,如:
①相关指数R2接近1,说明模型拟合效果好;
②表明残差平方和接近0,说明模型拟合效果好;
③表明“解析变量和预报变量的线性相关性强”;
④表明“广告费支出解析了98%的销售额变化。而随机误差贡献了2%”,所以广告费支出
对销售额的效应比随机误差的效应大得多. 14分.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目



 )如下表,以了解二者的关系。
)如下表,以了解二者的关系。 ,则
,则

 和
和 的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程
的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程 和
和 ,两人计算知
,两人计算知 相同,
相同, 也相同,下列正确的是( )
也相同,下列正确的是( )
 =1.23x+4
=1.23x+4


