题目内容
【题目】(1).公路上![]() 、
、![]() 两镇相距5公里,
两镇相距5公里,![]() 、
、![]() 往外各有两条叉路成
往外各有两条叉路成![]() 形状,计划在每条叉路上各建一加油站,要求每个站到
形状,计划在每条叉路上各建一加油站,要求每个站到![]() 、
、![]() 镇及其他站(沿公路进过
镇及其他站(沿公路进过![]() 、
、![]() 镇)距离互不相同,且距离均为整数公里,最长不超过15公里,此计划能否实现?
镇)距离互不相同,且距离均为整数公里,最长不超过15公里,此计划能否实现?
(2).若![]() 、
、![]() 向外各有3条叉路,欲建六个加油站,依然要求站与镇,站与站之间距离互不相同且为整数公路,最长者不超过28公里,能否实现?为什么?
向外各有3条叉路,欲建六个加油站,依然要求站与镇,站与站之间距离互不相同且为整数公路,最长者不超过28公里,能否实现?为什么?
【答案】(1)能(2)不能
【解析】
(1)两叉路情况可以实现.
如图所示:

其四站两镇间有![]() 种距离恰好互不相同,分别为
种距离恰好互不相同,分别为![]() 公里.
公里.
(2)三叉路情况不能实现,假设图中六站合要求,

到![]() 、
、![]() 距离为
距离为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,因有
,因有![]() 种不同距离,
种不同距离,
其总和为![]() (公里).
(公里).
在总和中,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 各被计算7次,而
各被计算7次,而![]() ,则共被计算16次,
,则共被计算16次,
故有等式![]() ,
,
由上式有![]() 这不成立,故不能实现.
这不成立,故不能实现.
注:上述方法在![]() (公里)时,不适用(∵
(公里)时,不适用(∵![]() 成立),其实,对
成立),其实,对![]() 为任意给定距离均不可实现.
为任意给定距离均不可实现.
下面介绍普遍证法:
设六个站建成如图.

在![]() 点记“
点记“![]() ”号,凡到
”号,凡到![]() 距离为偶数公里的点均记“
距离为偶数公里的点均记“![]() ”号,凡到
”号,凡到![]() 为奇数公里的点均记“
为奇数公里的点均记“![]() ”号,
”号,
于是,![]() 、
、![]() 及六个站均记上“
及六个站均记上“![]() ”或“
”或“![]() ”号,且同号两点距离为偶数,异号两点间距离为奇数,设有
”号,且同号两点距离为偶数,异号两点间距离为奇数,设有![]() 个“
个“![]() ”号,
”号,![]() 个“
个“![]() ”号,
”号,
则![]() , ①
, ①
又因奇数距离共![]() 个,而
个,而![]() 间奇数有14个,
间奇数有14个,
于是,![]() , ②
, ②
但满足方程组①②的整数解![]() 、
、![]() 不存在,
不存在,
故三叉路修站计划不能实现.

【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,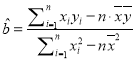 ,
,![]() ,
,![]() .
.
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)用对数回归模型拟合y与x的关系,可得回归方程:![]() ,经计算得出线性回归模型和对数模型的
,经计算得出线性回归模型和对数模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.

