Question

【题目】某超市销售某种商品，据统计，该该商品每日的销售量（单位：千克）与销售价格（单位：元/千克，其中）满足：当时，（，为常数）；当时，，已知当销售价格为6元/千克时，每日售出该商品170千克.

（1）求，的值，并确定关于的函数解析式；

（2）若该商品的销售成本为3元/千克，试确定销售价格的值，使店铺每日销售该商品所获利润最大.

Answer 1

【答案】（1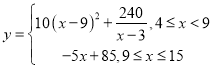），；（2）销售价格为5元/千克时，每日利润最大所获利润，最大

【解析】

（1）由题意，代入数据求出，；从而求出函数的解析式；

（2）由于是分段函数，讨论其各部分的最大值，从而求函数的最大值点．

（1）因为时，；又时，，

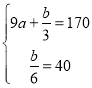∴，解得.

故每日的销售量.

（2）由（1）知，当时，每日销售利润

∴.

当时，单调递增；

当时，单调递减；

∴是函数在上的唯一极大值点，

∴；

当时，每日销售利润，

∴.

∵，∴销售价格为5元/千克时，每日利润最大.