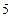题目内容
设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx, sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间;
(2)当x∈[0, ]时,f(x)的最大值为4,求m的值.
]时,f(x)的最大值为4,求m的值.
 sin2x+m).
sin2x+m).(1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间;
(2)当x∈[0,
 ]时,f(x)的最大值为4,求m的值.
]时,f(x)的最大值为4,求m的值.(1)单调递增区间为[0,  ],[+
],[+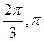 ] (2)1
] (2)1
 ],[+
],[+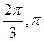 ] (2)1
] (2)1(1)∵f(x)=2cos2x+ sin2x+m=2sin(2x+
sin2x+m=2sin(2x+ )+m+1,
)+m+1,
∴函数f(x)的最小正周期T=π.
在[0, π]上单调递增区间为[0, ],[+
],[+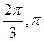 ]
]
(2)当x∈[0, ]时,∵f(x)递增,∴当x=
]时,∵f(x)递增,∴当x= 时,f(x)最大值为m+3=4,即m+3=4,
时,f(x)最大值为m+3=4,即m+3=4,
解得m=1∴m的值为1.
 sin2x+m=2sin(2x+
sin2x+m=2sin(2x+ )+m+1,
)+m+1,∴函数f(x)的最小正周期T=π.
在[0, π]上单调递增区间为[0,
 ],[+
],[+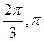 ]
](2)当x∈[0,
 ]时,∵f(x)递增,∴当x=
]时,∵f(x)递增,∴当x= 时,f(x)最大值为m+3=4,即m+3=4,
时,f(x)最大值为m+3=4,即m+3=4,解得m=1∴m的值为1.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 ,cos(α+β)=1,求证:cos(2α+β)=
,cos(α+β)=1,求证:cos(2α+β)= ,则
,则 的最大值是
的最大值是 B.
B. C.
C. D.
D.
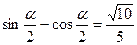 ,
, ,求
,求 的值.
的值. .
. 的单调性;
的单调性; ,则
,则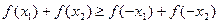 .
. ,
, .
. 的值;
的值;  的值.
的值.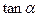 =2,求:
=2,求: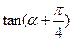 的值; (2)
的值; (2)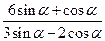 的值.
的值. 且
且 .求
.求 的值.
的值. 的最大值是( ).
的最大值是( ).