题目内容
（2007•温州一模）a，b为正实数是a2+b2≥2ab的（ ）
分析：当a，b为正实数时一定可以看出重要不等式成立，当a2+b2≥2ab成立时，不一定推出a，b都是正数，这里对数字的正负没有限制，故前者可以推出后者，而后者不能推出前者．
解答：解：∵当a，b为正实数时一定可以看出重要不等式成立，
当a2+b2≥2ab成立时，不一定推出a，b都是正数，这里对数字的正负没有限制，
故前者可以推出后者，而后者不能推出前者，
∴前者是后者的充分不必要条件，
故选A．
当a2+b2≥2ab成立时，不一定推出a，b都是正数，这里对数字的正负没有限制，
故前者可以推出后者，而后者不能推出前者，
∴前者是后者的充分不必要条件，
故选A．
点评：本题考查充要条件、必要条件与充分条件，及重要不等式，本题解题的关键是理解重要不等式使用的条件，本题是一个基础题．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
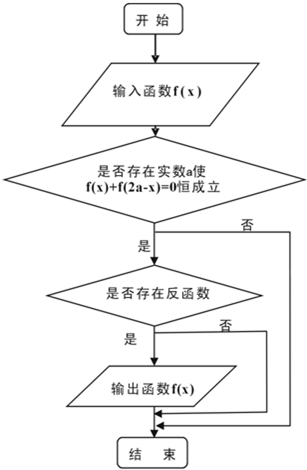（2007•温州一模）某流程如图所示，现输入如下四个函数，则可以输出的函数是（ ）