题目内容
若对可导函数f(x)，g(x)，当x∈[0,1]时恒有f′(x)·g(x)<f(x)·g′(x)，若已知α，β是一个锐角三角形的两个内角，且α≠β，记F(x)＝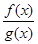
(g(x)≠0)，则下列不等式正确的是( )
A．F(cosα)>F(cosβ) B．F(cosα)<F(cosβ) C．F(sinα)<F(cosβ) D．F(sinα)>F(sinβ)
【答案】
C
【解析】∵F(x)＝
，∴
，∴函数F(x)为单调减函数，又α，β是锐角且
，∴
，∴
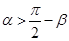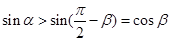，∴F(sinα)<F(cosβ)，故选C
练习册系列答案
相关题目
若对可导函数f（x），g（x），当x∈[0，1]时恒有f′（x）•g（x）＜f（x）•g′（x），若已知α，β 是一锐角三角形的两个内角，且α≠β，记F′（x）=
(g(x)≠0)，则下列不等式正确的是（ ）
| f(x) |
| g(x) |
| A、F（sinα）＜F（cosβ） |
| B、F（sinα）＜F（sinβ） |
| C、F（cosα）＞F（cosβ） |
| D、F（cosα）＜F（cosβ） |
，已知α、β是一个锐角三角形
的两个内角，且α≠β，记F（x）=
(g(x)
≠0)，则下列不等式正确的是（ ）
osβ) D．F(cosα)<
F(cosβ)