题目内容
已知点(
,2)在幂函数f(x)的图象上,点(
,
)在幂函数g(x)的图象上.
(1)求函数f(x),g(x)的解析式;
(2)作出这两个函数的草图,观察当x取何值时,f(x)>g(x).
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
(1)求函数f(x),g(x)的解析式;
(2)作出这两个函数的草图,观察当x取何值时,f(x)>g(x).
分析:(1)设f(x)=xa,g(x)=xm,由点(
,2)在幂函数f(x)的图象上,点(
,
)在幂函数g(x)的图象上,代入可求a,m从而可求f(x),g(x)
(2)结合函数的图象可求满足f(x)>g(x)时的x取值集合即可
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
(2)结合函数的图象可求满足f(x)>g(x)时的x取值集合即可
解答: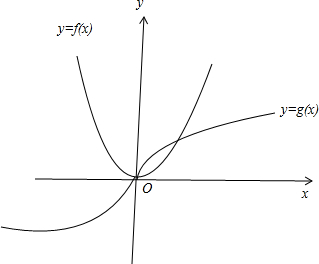 解:(1)设f(x)=xa,g(x)=xm
解:(1)设f(x)=xa,g(x)=xm
由点(
,2)在幂函数f(x)的图象上,点(
,
)在幂函数g(x)的图象上
∴2=(
)a,
=(
)m
∴a=2,m=
∴f(x)=x2,g(x)=x
,…(5分)
(2)结合函数的图象可知,函数f(x)=x2,g(x)=x
,有2个交点
由
可得x=0或x=1,即交点(0,0),(1,1)
结合函数图象可知,当x<0,或x>1时,f(x)>g(x)…(10分)
 解:(1)设f(x)=xa,g(x)=xm
解:(1)设f(x)=xa,g(x)=xm由点(
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
∴2=(
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
∴a=2,m=
| 1 |
| 3 |
∴f(x)=x2,g(x)=x
| 1 |
| 3 |
(2)结合函数的图象可知,函数f(x)=x2,g(x)=x
| 1 |
| 3 |
由
|
结合函数图象可知,当x<0,或x>1时,f(x)>g(x)…(10分)
点评:本题主要考查了幂函数的解析式的求解,幂函数的图象的作法及利用函数的图象求解不等式,属于中档试题

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目