题目内容

在同一平面直角坐标系中，函数y=cos(
x
2
+
3π
2
)（x∈[0，2π]）的图象和直线y=
1
2
的交点个数是（　　）
A、0B、1C、2D、4
分析：先根据诱导公式进行化简，再由x的范围求出
x
2
的范围，再由正弦函数的图象可得到答案．
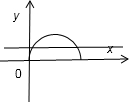解答：精英家教网解：原函数可化为：y=cos（
x
2
+
3π
2
）（x∈[0，2π]）=sin
x
2
，x∈[0，2π]．
当x∈[0，2π]时，
x
2
∈[0，π]，其图象如图，
与直线y=
1
2
的交点个数是2个．
故选C．
点评：本小题主要考查三角函数图象的性质问题．
练习册系列答案
相关题目
在同一平面直角坐标系中，函数y=g（x）的图象与y=ex的图象关于直线y=x对称．而函数y=f（x）的图象与y=g（x）的图象关于y轴对称，若f（m）=-1，则m的值是（　　）
A、-e
B、-
1
e
C、e
D、
1
e
函数y=ln|
1
x
|与y=-
x2+1
在同一平面直角坐标系内的大致图象为（　　）
函数y=ln|
1
x
|与y=-
-x2+1
在同一平面直角坐标系内的大致图象为（　　）
在同一平面直角坐标系中，画出函数u（x）=3sinx-cosx，v（x）=sin（2x）+3cos（2x），φ（x）=2sinx+2cosx的部分图象如下，则（　　）
（2012•虹口区二模）在同一平面直角坐标系中，函数y=g（x）的图象与y=3x的图象关于直线y=x对称，而函数y=f（x）的图象与y=g（x）的图象关于y轴对称，若f（a）=-1，则a的值是
-
1
3
-
1
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网