题目内容
设函数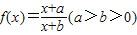 .
.(I)证明f(x)在(-b,+∞)内是减函数;
(II)若不等式
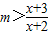 在[4,6]上恒成立,求实数m的取值范围.
在[4,6]上恒成立,求实数m的取值范围.
【答案】分析:(I)设x1>x2>-b,然后判定f(x1)-f(x2)的符号,根据函数单调性的定义进行判定即可;
(II)根据(I)可知函数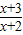 在(-2,+∞)上单调递减,从而得到在[4,6]上的单调性,从而可求出最值,即可求出所求.
在(-2,+∞)上单调递减,从而得到在[4,6]上的单调性,从而可求出最值,即可求出所求.
解答:(I)证明:f(x)=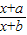 =1+
=1+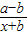
设x1>x2>-b,
则f(x1)-f(x2)=1+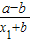 -(1-
-(1-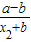 )=
)=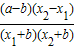 ;
;
∵a>b>0,x1>x2>-b
∴a-b>0,x2-x1<0,x1+b>0,x2+b>0
则f(x1)-f(x2)<0
∴f(x)在(-b,+∞)内是减函数;
(II)∵不等式 在[4,6]上恒成立
在[4,6]上恒成立
∴m>(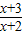 )max
)max
而由(1)可知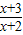 在(-2,+∞)上单调递减则在[4,6]上减
在(-2,+∞)上单调递减则在[4,6]上减
∴m>(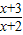 )max=
)max=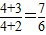 .
.
点评:本题主要考查了分式函数的单调性,以及恒成立问题,同时考查了等价转化的思想和运算求解的能力,属于中档题.
(II)根据(I)可知函数
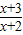 在(-2,+∞)上单调递减,从而得到在[4,6]上的单调性,从而可求出最值,即可求出所求.
在(-2,+∞)上单调递减,从而得到在[4,6]上的单调性,从而可求出最值,即可求出所求.解答:(I)证明:f(x)=
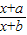 =1+
=1+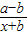
设x1>x2>-b,
则f(x1)-f(x2)=1+
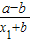 -(1-
-(1-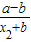 )=
)=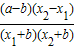 ;
;∵a>b>0,x1>x2>-b
∴a-b>0,x2-x1<0,x1+b>0,x2+b>0
则f(x1)-f(x2)<0
∴f(x)在(-b,+∞)内是减函数;
(II)∵不等式
 在[4,6]上恒成立
在[4,6]上恒成立∴m>(
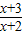 )max
)max而由(1)可知
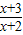 在(-2,+∞)上单调递减则在[4,6]上减
在(-2,+∞)上单调递减则在[4,6]上减∴m>(
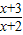 )max=
)max=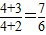 .
.点评:本题主要考查了分式函数的单调性,以及恒成立问题,同时考查了等价转化的思想和运算求解的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.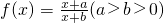 .
.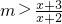 在[4,6]上恒成立,求实数m的取值范围.
在[4,6]上恒成立,求实数m的取值范围. .
. 在[4,6]上恒成立,求实数m的取值范围.
在[4,6]上恒成立,求实数m的取值范围. .
.