题目内容
设函数
．
（I）证明f（x）在（﹣b，+∞）内是减函数；
（II）若不等式
在[4，6]上恒成立，求实数m的取值范围．
．（I）证明f（x）在（﹣b，+∞）内是减函数；
（II）若不等式
在[4，6]上恒成立，求实数m的取值范围．（I）证明：f（x）=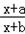
=1+
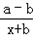
设x1＞x2＞﹣b，
则f（x1）﹣f（x2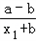）=1+
﹣（1﹣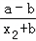
）=
；
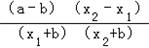∵a＞b＞0，x1＞x2＞﹣b
∴a﹣b＞0，x2﹣x1＜0，x1+b＞0，x2+b＞0
则f（x1）﹣f（x2）＜0
∴f（x）在（﹣b，+∞）内是减函数；
（II）∵不等式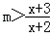
在[4，6]上恒成立
∴m＞（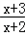
）max
而由（1）可知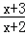
在（﹣2，+∞）上单调递减则在[4，6]上减
∴m＞（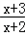
）max =
．
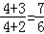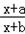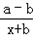
=1+设x1＞x2＞﹣b，
则f（x1）﹣f（x2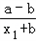）=1+
﹣（1﹣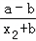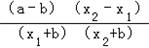）=；∵a＞b＞0，x1＞x2＞﹣b
∴a﹣b＞0，x2﹣x1＜0，x1+b＞0，x2+b＞0
则f（x1）﹣f（x2）＜0
∴f（x）在（﹣b，+∞）内是减函数；
（II）∵不等式
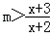在[4，6]上恒成立∴m＞（
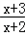）max而由（1）可知
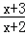在（﹣2，+∞）上单调递减则在[4，6]上减∴m＞（
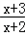）max =．
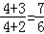练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
．
．
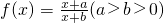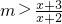在[4，6]上恒成立，求实数m的取值范围．
．
．
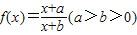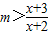在[4，6]上恒成立，求实数m的取值范围．