Question

8．一艘船以4km/h的速度沿着与水流方向成120°夹角的方向航行，已知河水流速为2km/h，则经过$\sqrt{3}$ h，该船的实际航程为（　　）

• A． 2$\sqrt{15}$ km
• B． 6 km
• C． 2$\sqrt{21}$ km
• D． 8 km

Answer 1

分析 根据题意，画出示意图，根据三角形的知识求出解来．

解答 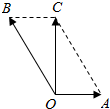解：如图所示，$\overrightarrow{OA}$表示水流速度，$\overrightarrow{OB}$表示船在静水中的速度，
则$\overrightarrow{OC}$表示船的实际速度；
又|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=4，∠AOB=120°，则∠CBO=60°，
∴|$\overrightarrow{OC}$|=2$\sqrt{3}$，∠AOC=∠BCO=90°
∴实际速度为2$\sqrt{3}$km/h，则实际航程为2$\sqrt{3}$×$\sqrt{3}$=6km．
故选：B．

点评 本题考查了平面向量的应用问题，解题时应注意船在静水中的速度，水流速度和船的实际速度的区别，是基础题目．