题目内容
在平面直角坐标系
中，点
的坐标分别是（0，-3），（0,3），直线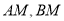
相交于点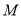
，且它们的斜率之积是
.
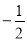（1）求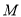
的轨迹
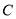方程；
（2）若直线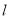
经过点
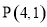，与轨迹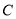
有且仅有一个公共点，求直线
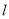的方程.
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
七彩题卡口算应用一点通系列答案题目内容
在平面直角坐标系中，点的坐标分别是（0，-3），（0,3），直线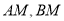相交于点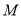，且它们的斜率之积是.
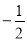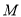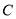（1）求的轨迹方程；
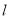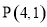（2）若直线经过点，与轨迹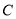有且仅有一个公共点，求直线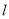的方程.
七彩题卡口算应用一点通系列答案
的离心率
，过椭圆的左焦点
且倾斜角为30°的直线与圆
相交所得弦的长度为1.
的方程；
交椭圆
于不同两点
，设
，
为坐标原点.当以线段
为直径的圆恰好过点
时，求证：
的面积为定值，并求出该定值.
，
，其中
为虚数单位，则
（ ）
B．
D．
，下列结论错误的是（ ）
的最小正周期为
对称 
上是减函数 
对称
，
，则
（ ）
B．
C．
D．
满足约束条件
，若目标函数
的最大值为1，则
的最小值为 ．
的前
项和为
，若
，则
等于（ ）
，若
，则
．
，则实数
均为0”的逆命题；
，则
”的逆否命题；