题目内容
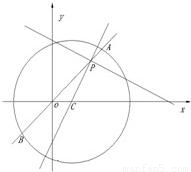
 如图,圆C:x2-(1+a)x+y2-ay+a=0.
如图,圆C:x2-(1+a)x+y2-ay+a=0.(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知a>1,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M任作一条直线与圆O:x2+y2=4相交于两点A,B.问:是否存在实数a,使得∠ANM=∠BNM?若存在,求出实数a的值,若不存在,请说明理由.
分析:(Ⅰ)在圆的方程中,令y=0,可得关于x的一元二次方程的判别式等于零,由此求得a的值,从而求得所求圆C的方程.
(Ⅱ)先求出所以M(1,0),N(a,0),假设存在实数a,当直线AB与x轴不垂直时,设直线AB的方程为y=k(x-1),代入x2+y2=4,利用韦达定理,根据NA、NB的斜率之和等于零求得a的值.经过检验,当直线AB与x轴垂直时,这个a值仍然满足∠ANM=∠BNM,从而得出结论.
(Ⅱ)先求出所以M(1,0),N(a,0),假设存在实数a,当直线AB与x轴不垂直时,设直线AB的方程为y=k(x-1),代入x2+y2=4,利用韦达定理,根据NA、NB的斜率之和等于零求得a的值.经过检验,当直线AB与x轴垂直时,这个a值仍然满足∠ANM=∠BNM,从而得出结论.
解答:(Ⅰ)因为由
可得x2-(1+a)x+a=0,
由题意得△=(1+a)2-4a=(a-1)2=0,所以a=1,
故所求圆C的方程为x2-2x+y2-y+1=0.
(Ⅱ)令y=0,得x2-(1+a)x+a=0,即(x-1)(x-a)=0,求得x=1,或x=a,
所以M(1,0),N(a,0).
假设存在实数a,当直线AB与x轴不垂直时,设直线AB的方程为y=k(x-1),
代入x2+y2=4得,(1+k2)x2-2k2x+k2-4=0,
设A(x1,y1),B(x2,y2),从而x1+x2=
,x1x2=
.
因为NA、NB的斜率之和为
+
=
,
而(x1-1)(x2-a)+(x2-1)(x1-a)=2x1x2-(a+1)(x2+x1)+2a=2
-(a+1)
+2a=
,
因为∠ANM=∠BNM,所以,NA、NB的斜率互为相反数,
+
=0,即
=0,得a=4.
当直线AB与x轴垂直时,仍然满足∠ANM=∠BNM,即NA、NB的斜率互为相反数.
综上,存在a=4,使得∠ANM=∠BNM.
|
由题意得△=(1+a)2-4a=(a-1)2=0,所以a=1,
故所求圆C的方程为x2-2x+y2-y+1=0.
(Ⅱ)令y=0,得x2-(1+a)x+a=0,即(x-1)(x-a)=0,求得x=1,或x=a,
所以M(1,0),N(a,0).
假设存在实数a,当直线AB与x轴不垂直时,设直线AB的方程为y=k(x-1),
代入x2+y2=4得,(1+k2)x2-2k2x+k2-4=0,
设A(x1,y1),B(x2,y2),从而x1+x2=
| 2k2 |
| 1+k2 |
| k2-4 |
| 1+k2 |
因为NA、NB的斜率之和为
| y1 |
| x1-a |
| y2 |
| x2-a |
| k[(x1-1)(x2-a)+(x2-1)(x1-a)] |
| (x1-a)(x2-a) |
而(x1-1)(x2-a)+(x2-1)(x1-a)=2x1x2-(a+1)(x2+x1)+2a=2
| k2-4 |
| 1+k2 |
| 2k2 |
| 1+k2 |
| 2a-8 |
| 1+k2 |
因为∠ANM=∠BNM,所以,NA、NB的斜率互为相反数,
| y1 |
| x1-a |
| y2 |
| x2-a |
| 2a-8 |
| 1+k2 |
当直线AB与x轴垂直时,仍然满足∠ANM=∠BNM,即NA、NB的斜率互为相反数.
综上,存在a=4,使得∠ANM=∠BNM.
点评:本题主要考查求圆的标准方程,直线和圆的位置关系,直线的倾斜角和斜率,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,圆C:x2+y2-2x-8=0内有一点P(2,2),过点p作直线l交圆于A,B两点.
如图,圆C:x2+y2-2x-8=0内有一点P(2,2),过点p作直线l交圆于A,B两点.
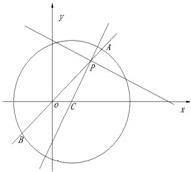 如图,圆C:x2+y2-2x-8=0内有一点P(2,2),过点p作直线l交圆于A,B两点.
如图,圆C:x2+y2-2x-8=0内有一点P(2,2),过点p作直线l交圆于A,B两点.