Question

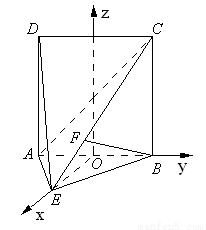
（本小题满分12分）如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.

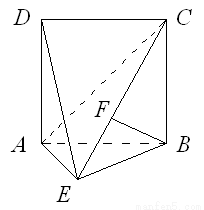
（I）求证AE⊥平面BCE；

（Ⅱ）求二面角B—AC—E的大小；

（Ⅲ）求点D到平面ACE的距离.

 

Answer 1

【答案】

解：（1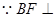）平面ACE.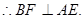   

∵二面角D—AB—E为直二面角，且，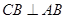

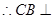平面ABE.

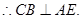
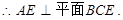  ……………………… 4分

（2）以线段AB的中点为原点O，OE所在直线为x轴，

AB所在直线为y轴，过O点平行于AD的直线为z轴，

建立空间直角坐标系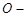xyz，如图.

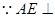面BCE，B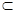E面BCE， ，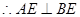

在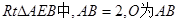的中点，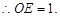

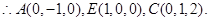
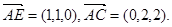 设平面AEC的一个法向量为，

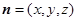则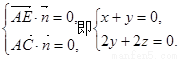 解得  

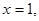令得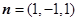是平面AEC的一个法向量. ………… 6分

又平面ABC的一个法向量为，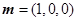

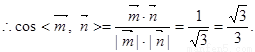 ………………………………………… 7分

∴二面角B—AC—E的大小为 ………………………………………… 8分

（3）∵AD // z轴，AD=2，∴，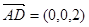

∴点D到平面ACE的距离

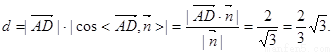  ……………………… 12分

【解析】略