题目内容
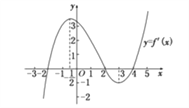
【题目】函数![]() 的导函数的图象如图所示,给出下列判断:
的导函数的图象如图所示,给出下列判断:
①函数![]() 在区间
在区间![]() 内单调递增;②函数
内单调递增;②函数![]() 在区间
在区间![]() 内单调递减;③函数
内单调递减;③函数![]() 在区间
在区间![]() 内单调递增;④当
内单调递增;④当![]() 时,函数
时,函数![]() 有极小值;⑤当
有极小值;⑤当![]() 时,函数
时,函数![]() 有极大值.则上述判断中正确的是( )
有极大值.则上述判断中正确的是( )
A. ①② B. ③
C. ②③ D. ③④⑤
【答案】B
【解析】对于命题①,因为在区间![]() ,导数值有正也有负,所以单调递增、单调递减都有可能,故不正确;对于命题②,在区间
,导数值有正也有负,所以单调递增、单调递减都有可能,故不正确;对于命题②,在区间![]() 上导数值有正也有负,所以函数单调递增、单调递减都有可能,故不正确;对于命题③,由于在区间
上导数值有正也有负,所以函数单调递增、单调递减都有可能,故不正确;对于命题③,由于在区间![]() 上导函数的值是正的,故单调递增,命题正确;对于命题④,当
上导函数的值是正的,故单调递增,命题正确;对于命题④,当 ![]() 时,导函数值是正的,当
时,导函数值是正的,当 ![]() 时,导函数值是负的,所以
时,导函数值是负的,所以![]() 取极大值,故命题不正确;对于命题⑤,由于
取极大值,故命题不正确;对于命题⑤,由于![]() 不是极值点,故函数
不是极值点,故函数![]() 没有极值,因此命题是错误的,应选答案B。
没有极值,因此命题是错误的,应选答案B。

练习册系列答案
相关题目
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.