题目内容
【题目】如图,正方形ABCD中边长为1,P、Q分别为BC、CD上的点,△CPQ周长为2. 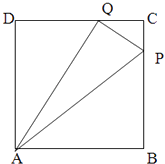
(1)求PQ的最小值;
(2)试探究求∠PAQ是否为定值,若是给出证明;不是说明理由.
【答案】
(1)解:设∠CPQ=θ,则CP=PQcosθ,CQ=PQsinθ
![]() (
( ![]() )
)
∴ 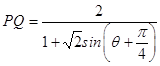
∴ ![]()
(2)解:分别以AB,AD所在直线为x轴、y轴建立平面直角坐标系,
设Q(x,1),P(1,y),设∠DAQ=α,∠PAB=β
∴ ![]() ,即xy+(x+y)=1
,即xy+(x+y)=1
又tanα=x,tanβ=y
∴ ![]() ,
,
∴ ![]()
∴ ![]()
【解析】(1)根据△CPQ周长为2,并且△CPQ是直角三角形,设∠CPQ=θ,根据三角函数的定义,CP=PQcosθ,CQ=PQsinθ,因此可以表示出 ![]() ,求该函数的最小值即可;(2)利用解析法求解:分别以AB,AD所在直线为x轴、y轴建立平面直角坐标系,设Q(x,1),P(1,y),利用两点间距离公式求出PQ,根据△CPQ周长为2,找出x,y的关系,求出∠PAQ的正切值,即可求得结果.
,求该函数的最小值即可;(2)利用解析法求解:分别以AB,AD所在直线为x轴、y轴建立平面直角坐标系,设Q(x,1),P(1,y),利用两点间距离公式求出PQ,根据△CPQ周长为2,找出x,y的关系,求出∠PAQ的正切值,即可求得结果.
【考点精析】根据题目的已知条件,利用两角和与差的正弦公式和两角和与差的正切公式的相关知识可以得到问题的答案,需要掌握两角和与差的正弦公式:![]() ;两角和与差的正切公式:
;两角和与差的正切公式:![]() .
.

练习册系列答案
相关题目