题目内容
偶函数f(x)满足f(x-1)=f(x+1),且在x∈[0,1]时,f(x)=x2,则关于x的 在
在 上根的个数是( )
上根的个数是( )A.1个
B.2个
C.3个
D.4个
【答案】分析:利用条件得f(x)=x2,x∈[-1,1],又周期为2,可以画出其在整个定义域上的图象,利用数形结合可得结论.
解答: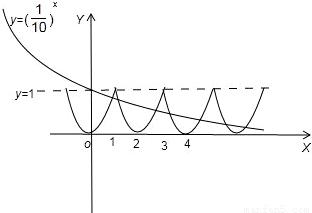 解;∵f(x-1)=f(x+1)⇒周期为2,
解;∵f(x-1)=f(x+1)⇒周期为2,
又∵在x∈[0,1]时,f(x)=x2,且f(x)是偶函数得f(x)=x2,x∈[-1,1],
∴f(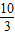 )=f(
)=f(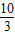 -4)=f(-
-4)=f(- )=f(
)=f( ),
),
由图知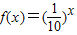 在[0,3]上根的个数是3个
在[0,3]上根的个数是3个
∵y=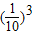 =
=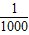 <f(
<f( )=
)= ,
,
∴知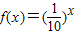 在[3,
在[3,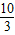 ]上根的个数是0个
]上根的个数是0个
故关于x的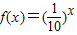 在
在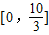 上根的个数是3个.
上根的个数是3个.
故选 C.
点评:本题考查了数形结合的数学思想,数形结合的应用大致分两类:一是以形解数,即借助数的精确性,深刻性来讲述形的某些属性;二是以形辅数,即借助与形的直观性,形象性来揭示数之间的某种关系,用形作为探究解题途径,获得问题结果的重要工具
解答:
 解;∵f(x-1)=f(x+1)⇒周期为2,
解;∵f(x-1)=f(x+1)⇒周期为2,又∵在x∈[0,1]时,f(x)=x2,且f(x)是偶函数得f(x)=x2,x∈[-1,1],
∴f(
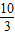 )=f(
)=f(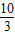 -4)=f(-
-4)=f(- )=f(
)=f( ),
),由图知
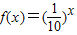 在[0,3]上根的个数是3个
在[0,3]上根的个数是3个∵y=
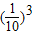 =
=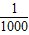 <f(
<f( )=
)= ,
,∴知
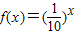 在[3,
在[3,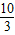 ]上根的个数是0个
]上根的个数是0个故关于x的
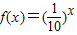 在
在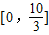 上根的个数是3个.
上根的个数是3个.故选 C.
点评:本题考查了数形结合的数学思想,数形结合的应用大致分两类:一是以形解数,即借助数的精确性,深刻性来讲述形的某些属性;二是以形辅数,即借助与形的直观性,形象性来揭示数之间的某种关系,用形作为探究解题途径,获得问题结果的重要工具

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0.则( )
| f(x2)-f(x1) |
| x2-x1 |
| A、f(3)<f(-2)<f(1) |
| B、f(1)<f(-2)<f(3) |
| C、f(-2)<f(1)<f(3) |
| D、f(3)<f(1)<f(-2) |
定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上单调递增,a=f(3),b=f(
),c=f(2),则a,b,c大小关系是( )
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、b>c>a |
| D、c>b>a |