题目内容
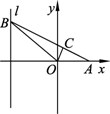
(经典回放)如图所示,给出定点A(a,0)(a>0)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
答案:
解析:
解析:
|
解析:依题意,记B(-1,b)(b∈R),则直线OA和OB的方程分别为y=0和y=-bx.设点C(x,y),则有0≤x<a,由OC平分∠AOB,知点C到OA、OB距离相等.根据点到直线的距离公式得 |y|= 依题设,点C在直线AB上,故有y= b= 将②式代入①式得y2[ 整理得y2[(1-a)x2-2ax+(1+a)y2]=0. 若y≠0,则(1-a)x2-2ax+(1+a)y2=0(0<x<a); 若y=0,则b=0,∠AOB=π,点C的坐标为(0,0),满足上式. 综上,得点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a). ∵a≠1, ∴ 由此知,当0<a<1时,方程③表示椭圆弧段; 当a>1时,方程③表示双曲线一支的弧段. |

练习册系列答案
相关题目
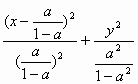 =1(0≤r<a).③
=1(0≤r<a).③
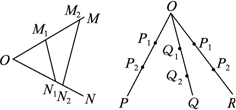
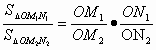 .若从点O所作的不在同一平面内的三条射线OP、OQ和OR上,分别有点P1、P2,点Q1、Q2和点R1、R2,则类似的结论为_________.
.若从点O所作的不在同一平面内的三条射线OP、OQ和OR上,分别有点P1、P2,点Q1、Q2和点R1、R2,则类似的结论为_________.