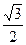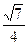题目内容
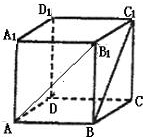
(本小题满分12分)如图,在棱长为2的正方体 的中点,P为BB1的中点.
的中点,P为BB1的中点.
(I)求证 ;
;
(II)求异面直线 所成角的大小;
所成角的大小;
 的中点,P为BB1的中点.
的中点,P为BB1的中点.(I)求证
 ;
;(II)求异面直线
 所成角的大小;
所成角的大小;
解法一:(I)连结BC1
由正方体的性质得BC1是BD1在
平面BCC1B1内的射影
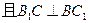 ,
,
所以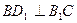
(II)又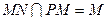 ,
,

(III)延长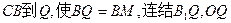
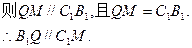
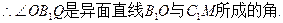
由于正方体的棱长为2,
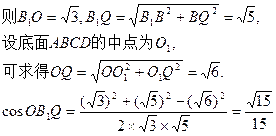
即异面直线 所成角的大小为arccos
所成角的大小为arccos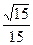 .
.
解法二:(I)如图建立空间直角坐标系.

则B(2,2,0),C(0,2,0)
B1(2,2,2),D1(0,0,2).
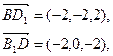 ………………3分
………………3分
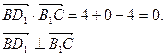
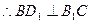 ……4分
……4分
(II)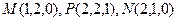 ,
,

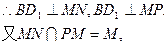
 . ……8分
. ……8分
(III)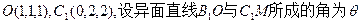 ,
,
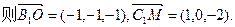
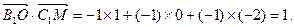
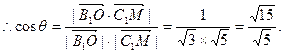
即异面直线 所成角的大小为arccso
所成角的大小为arccso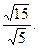 ……12分
……12分
由正方体的性质得BC1是BD1在
平面BCC1B1内的射影
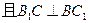 ,
,所以
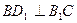
(II)又
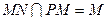 ,
,
(III)延长
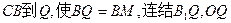
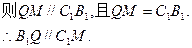
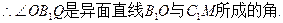
由于正方体的棱长为2,
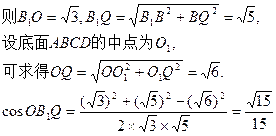
即异面直线
 所成角的大小为arccos
所成角的大小为arccos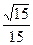 .
. 解法二:(I)如图建立空间直角坐标系.

则B(2,2,0),C(0,2,0)
B1(2,2,2),D1(0,0,2).
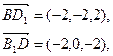 ………………3分
………………3分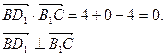
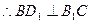 ……4分
……4分(II)
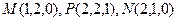 ,
,
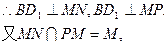
 . ……8分
. ……8分(III)
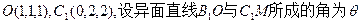 ,
,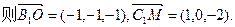
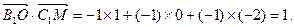
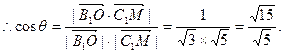
即异面直线
 所成角的大小为arccso
所成角的大小为arccso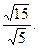 ……12分
……12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
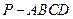 的底面是正方形,
的底面是正方形,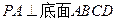 ,且
,且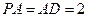 ,点
,点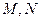 分别在侧棱
分别在侧棱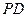 、
、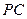 上,且
上,且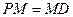 。
。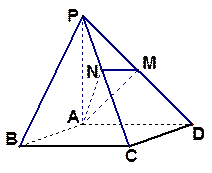
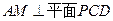 ;
;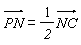 ,求平面
,求平面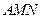 与平面
与平面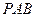 所成二面角的余弦值.
所成二面角的余弦值.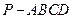 ,底面
,底面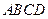 是边长为2的正方形,
是边长为2的正方形,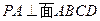 ,
,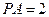 ,过点
,过点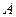 作
作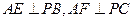 ,连接
,连接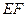 .
.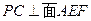 .
.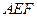 交侧棱
交侧棱 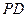 于点
于点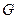 ,求多面体
,求多面体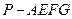 的体积。
的体积。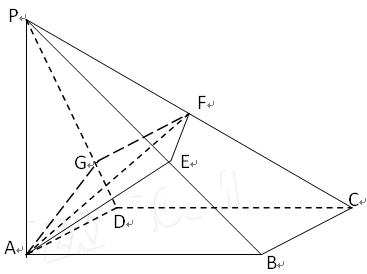
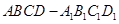 中,异面直线
中,异面直线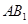 与
与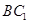 所成角的大小是( )
所成角的大小是( )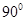
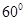
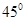
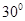
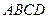 和矩形
和矩形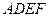 所在平面相互垂直,
所在平面相互垂直,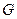 是
是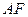 的中点.
的中点.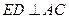 ;
;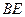 与平面
与平面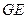 与
与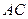 所成角的余弦值.
所成角的余弦值.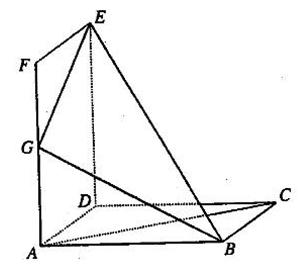
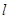 、
、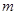 ,平面
,平面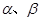 ,则下列命题中:
,则下列命题中:  ,
,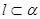 ,则
,则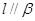
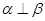 ,
,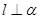 ,则
,则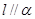 ,
,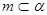 ,则
,则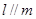
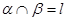 ,
, 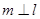 ,则
,则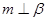 ,其中真命题有( )
,其中真命题有( )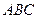 —
—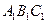 中,若∠BAC=
中,若∠BAC= ,
,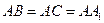 ,则异面直线
,则异面直线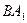 与
与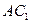 所成的角等于_________
所成的角等于_________