题目内容
下列推理是否正确,将有错误的指出错误之处.
(1)求证:四边形的内角和等于360°.
证明:设四边形ABCD为矩形,则四个角都是直角.
∴∠A+∠B+∠C+D=90°+90°+90°+90°=360°.
∴四边形的内角和为360°.
(2)已知![]() 和
和![]() 是无理数,试证:
是无理数,试证:![]() +
+![]() 也是无理数.
也是无理数.
证明:依题意知![]() 和
和![]() 都是无理数,而无理数与无理数的和是无理数,所以
都是无理数,而无理数与无理数的和是无理数,所以![]() +
+![]() 也必是无理数.
也必是无理数.
(3)在Rt△ABC中,∠C=90°,求证:a2+b2=c2.
证明:∵a=csinA,b=ccosA,
∴a2+b2=c2sin2A+c2cos2A=c2(sin2A+cos2A)=c2.
答案:
解析:
解析:
解:
上述三个推理过程都错(1)在证明过程中偷换论题,将四边形改为矩形,以偏概全;
(2)两无理数之和不一定为无理数;
(3)a=csinA,b=ccosA这些结论都是有前提的,是在直角三角形中才成立,犯了循环论证的错误
思路分析:判断论证的对错需看大前提、小前提是否都正确,证明过程中,不能偷换论题,不能循环论证,不能出现虚假论据,不能以偏概全

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
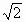 和
和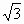 是无理数,试证:
是无理数,试证: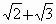 也是无理数.
也是无理数.
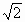 和
和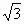 都是无理数,而无理数与无理数之和是无理数,所以
都是无理数,而无理数与无理数之和是无理数,所以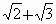 必是无理数.
必是无理数.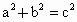 .
.
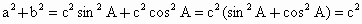 .
.