题目内容
在棱长为2的正方体AC1中,G是AA1的中点,则BD到平面GB1D1的距离是 .
【答案】分析:画出图形,根据线面平行的性质说明BD到平面GB1D1的距离,就是求O到O1G的距离,再结合解三角形的有关知识解三角形GOO1即可得到答案.
解答: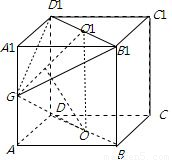 解:BD∥平面GB1D1,上下底面的中心分别为O1,O,
解:BD∥平面GB1D1,上下底面的中心分别为O1,O,
所以求BD到平面GB1D1的距离即求O到O1G的距离h,
由题意可得:GO=GO1= ;
;
在△GOO1中,GO=GO1=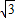 ,O1O=2,
,O1O=2,
所以O1O边上的高等于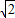 ,
,
所以根据等面积法可得: ,即
,即 ,
,
所以h=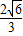 .
.
点评:本题考查正方体的线段间的距离,考查作图能力,转化思想.即由线到平面的距离,转化为点到平面的距离,进而转化为解三角形的问题,转化思想是求几何体的高,距离,是重要方法
解答:
 解:BD∥平面GB1D1,上下底面的中心分别为O1,O,
解:BD∥平面GB1D1,上下底面的中心分别为O1,O,所以求BD到平面GB1D1的距离即求O到O1G的距离h,
由题意可得:GO=GO1=
 ;
;在△GOO1中,GO=GO1=
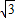 ,O1O=2,
,O1O=2,所以O1O边上的高等于
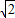 ,
,所以根据等面积法可得:
 ,即
,即 ,
,所以h=
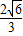 .
.点评:本题考查正方体的线段间的距离,考查作图能力,转化思想.即由线到平面的距离,转化为点到平面的距离,进而转化为解三角形的问题,转化思想是求几何体的高,距离,是重要方法

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
在棱长为2的正方体AC1中,G是AA1的中点,则BD到平面GB1D1的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( ) (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).
(2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).