题目内容
解下列不等式:
(1)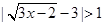 (2)
(2)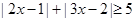
(1) 或
或 ;(2)
;(2) 或
或 .
.
解析试题分析:(1)首先要确保不等式中二次根式有意义,即需满足 ,又根据
,又根据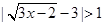 ,可得
,可得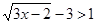 或
或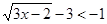 ,因此可以得到两个关于
,因此可以得到两个关于 的不等式组
的不等式组 或
或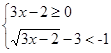 ,从而解得
,从而解得 或
或 ;(2)原不等式中涉及到两个绝对值号,只有利用分类讨论将其去掉,即分三种情况:①
;(2)原不等式中涉及到两个绝对值号,只有利用分类讨论将其去掉,即分三种情况:①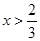 ,②
,② ,③
,③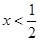 ,可以将两个绝对值号去掉,从而将绝对值不等式转化为关于
,可以将两个绝对值号去掉,从而将绝对值不等式转化为关于 的一元一次不等式.
的一元一次不等式.
(1)原不等式等价于 或
或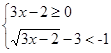 ,解得
,解得 或
或 ;
;
①若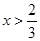 :则原不等式等价于
:则原不等式等价于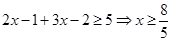 ;②若
;②若 :则原不等式等价于
:则原不等式等价于 ,解得
,解得 ,这与
,这与 矛盾,舍去;③若
矛盾,舍去;③若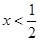 ,则原不等式等价于
,则原不等式等价于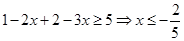 .综上所述,不等式的解为
.综上所述,不等式的解为 或
或 .
.
考点:绝对值不等式的解法.

练习册系列答案
相关题目
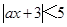 的解集为(-1,4),则实数a的值为_________.
的解集为(-1,4),则实数a的值为_________.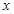 的不等式
的不等式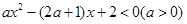 .
.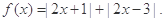
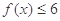 的解集;
的解集;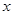 的不等式
的不等式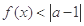 的解集非空,求实数
的解集非空,求实数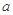 的取值范围.
的取值范围.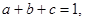
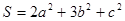 的最小值及取最小值时
的最小值及取最小值时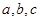 的值。
的值。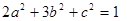 ,求
,求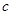 的取值范围。
的取值范围。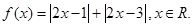 .
.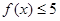 ;
;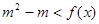 ,
, 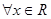 都成立,求实数
都成立,求实数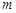 的取值范围.
的取值范围.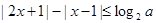 (其中
(其中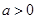 ).
).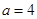 时,求不等式的解集;
时,求不等式的解集;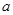 的取值范围
的取值范围