题目内容
以下是正弦函数的定义:
在平面直角坐标系中,设α的终边上任意一点P的坐标是(x,y),它与原点的距离是r (r>0),比值
叫做α的正弦,记作sinα,即sinα=
;
请使用此定义,证明:(1)正弦函数的值域为[-1,1];(2)函数f(α)=sinα是奇函数.
在平面直角坐标系中,设α的终边上任意一点P的坐标是(x,y),它与原点的距离是r (r>0),比值
| y |
| r |
| y |
| r |
请使用此定义,证明:(1)正弦函数的值域为[-1,1];(2)函数f(α)=sinα是奇函数.
分析:(1)当α的终边没有落在坐标轴上时,根据直角三角形的性质斜边大于直角边,即r>|y|,当α的终边落在x轴上时,y=0,当α的终边落在y轴上时,|y|=r,进而得到正弦函数的值域为[-1,1].
(2)由题意可得:函数f(α)=sinα的定义域为:R,并且得到f(-α)=
=-sinα=-f(α),进而得到此函数为奇函数.
(2)由题意可得:函数f(α)=sinα的定义域为:R,并且得到f(-α)=
| -y |
| r |
解答:解:(1)当α的终边没有落在坐标轴上时,根据直角三角形的性质斜边大于直角边,即r>|y|,
所以|
|<1,并且|
|≠0,
当α的终边落在x轴上时,y=0,此时|
|=0,
当α的终边落在y轴上时,|y|=r,此时|
|=1,
所以|
|≤1,即正弦函数的值域为[-1,1].
(2)由题意可得:函数f(α)=sinα的定义域为:R,
又因为f(-α)=
=-sinα=-f(α),即f(-α)=-f(α),
所以函数f(α)=sinα是奇函数.
所以|
| y |
| r |
| y |
| r |
当α的终边落在x轴上时,y=0,此时|
| y |
| r |
当α的终边落在y轴上时,|y|=r,此时|
| y |
| r |
所以|
| y |
| r |
(2)由题意可得:函数f(α)=sinα的定义域为:R,
又因为f(-α)=
| -y |
| r |
所以函数f(α)=sinα是奇函数.
点评:此题主要考查正弦函数的定义与有关的性质,以及考查奇函数的定义,并且能够利用定义证明函数的奇偶性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
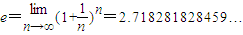 ,定义函数
,定义函数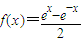 为双曲正弦函数,记为sinhx,定义函数
为双曲正弦函数,记为sinhx,定义函数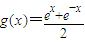 为双曲余弦函数,记为coshx.则以下三个命题正确的是 .(只需填正确命题序号)
为双曲余弦函数,记为coshx.则以下三个命题正确的是 .(只需填正确命题序号)