题目内容
常数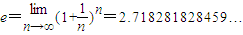 ,定义函数
,定义函数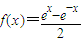 为双曲正弦函数,记为sinhx,定义函数
为双曲正弦函数,记为sinhx,定义函数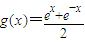 为双曲余弦函数,记为coshx.则以下三个命题正确的是 .(只需填正确命题序号)
为双曲余弦函数,记为coshx.则以下三个命题正确的是 .(只需填正确命题序号)(1)cosh(x+y)=coshx•coshy-sinhx•sinhy;
(2)sinh(x+y)=sinhx•coshy+coshx•sinhy;
(3)(sinhx)2-(coshx)2=1.
【答案】分析:(1)根据题中的新定义分别表示出cosh(x+y),coshx,coshy,sinhx,sinhy,利用同底数幂的乘法法则及多项式的乘法法则计算coshx•coshy-sinhx•sinhy,即可作出判断;
(2)根据题中的新定义分别表示出sinh(x+y),coshx,coshy,sinhx,sinhy,利用同底数幂的乘法法则及多项式的乘法法则计算sinhx•coshy+coshx•sinhy,即可作出判断;
(3)根据题中的新定义分别表示出sinhx,coshx,利用同底数幂的乘法法则及多项式的乘法法则计算(sinhx)2-(coshx)2,即可作出判断.
解答:解:(1)cosh(x+y)= ,
,
coshx•coshy-sinhx•sinhy
= •
•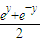 -
-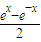 •
•
= ,
,
∴cosh(x+y)≠coshx•coshy-sinhx•sinhy,
故本选项错误;
(2)sinh(x+y)=
sinhx•coshy+coshx•sinhy
= •
• +
+ •
•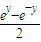
=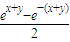 ,
,
故本选项正确;
(3)(sinhx)2-(coshx)2
=( )2-(
)2-( )2
)2
=-1≠1,
故本选项错误,
则三个命题正确的是(2).
故答案为:(2)
点评:此题考查了新定义的理解,解答此类题要切实对题中的新定义以正确的理解,这样才能对新定义下的运算熟练运用,注意新定义下对普通运算不一定成立,比如本题(1)对于两角和与差的余弦函数公式不成立,灵活运用题中的新定义是解本题的关键.
(2)根据题中的新定义分别表示出sinh(x+y),coshx,coshy,sinhx,sinhy,利用同底数幂的乘法法则及多项式的乘法法则计算sinhx•coshy+coshx•sinhy,即可作出判断;
(3)根据题中的新定义分别表示出sinhx,coshx,利用同底数幂的乘法法则及多项式的乘法法则计算(sinhx)2-(coshx)2,即可作出判断.
解答:解:(1)cosh(x+y)=
 ,
,coshx•coshy-sinhx•sinhy
=
 •
•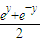 -
-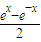 •
•
=
 ,
,∴cosh(x+y)≠coshx•coshy-sinhx•sinhy,
故本选项错误;
(2)sinh(x+y)=

sinhx•coshy+coshx•sinhy
=
 •
• +
+ •
•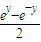
=
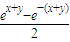 ,
,故本选项正确;
(3)(sinhx)2-(coshx)2
=(
 )2-(
)2-( )2
)2=-1≠1,
故本选项错误,
则三个命题正确的是(2).
故答案为:(2)
点评:此题考查了新定义的理解,解答此类题要切实对题中的新定义以正确的理解,这样才能对新定义下的运算熟练运用,注意新定义下对普通运算不一定成立,比如本题(1)对于两角和与差的余弦函数公式不成立,灵活运用题中的新定义是解本题的关键.

练习册系列答案
相关题目