题目内容
设[x]表示不超过x的最大整数,如 ,对于给定的n∈N*,定义
,对于给定的n∈N*,定义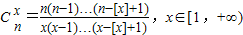 ,则当
,则当 时,函数
时,函数 的值域为 .
的值域为 .
【答案】分析:将区间 分为
分为 、[2,3)两段,分别求出函数值的范围后,综合讨论结果可得答案.
、[2,3)两段,分别求出函数值的范围后,综合讨论结果可得答案.
解答:解:当x∈ 时,
时, =
= =
= ,
,
当x无限接近2时,[x]=1,所以 =
= =4
=4
当[2,3)时,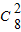 =
= =28
=28
x无限接近3时,[x]=2,
∴ =
=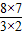 =
= ,
,
故函数C8x的值域是
故答案为: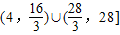
点评:本题主要考查已知函数解析式求函数值域的问题.求函数值域有时需要进行分段考虑.
 分为
分为 、[2,3)两段,分别求出函数值的范围后,综合讨论结果可得答案.
、[2,3)两段,分别求出函数值的范围后,综合讨论结果可得答案.解答:解:当x∈
 时,
时, =
= =
= ,
,当x无限接近2时,[x]=1,所以
 =
= =4
=4当[2,3)时,
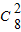 =
= =28
=28x无限接近3时,[x]=2,
∴
 =
=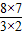 =
= ,
,故函数C8x的值域是

故答案为:
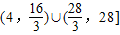
点评:本题主要考查已知函数解析式求函数值域的问题.求函数值域有时需要进行分段考虑.

练习册系列答案
相关题目
设[x]表示不超过x的最大整数(如[2]=2,[
]=1),对于给定的n∈N*,定义
=
,x∈[1,+∞),则当x∈[
,3)时,函数
的值域是( )
| 5 |
| 4 |
| C | x n |
| n(n-1)…(n-[x]+1) |
| x(x-1)…(x-[x]+1) |
| 3 |
| 2 |
| C | x 8 |
A、[
| ||||
B、[
| ||||
C、(4,
| ||||
D、(4,
|
设[x]表示不超过x的最大整数(如:[1]=1,[
]=2),则定义在[2,4)的函数f(x)=x[x]-ax(其中a为常数,且a≤4)的值域为( )
| 5 |
| 2 |
| A、[4-2a,64-4a) |
| B、[4-2a,9-3a)∪[27-3a,64-4a) |
| C、[9-3a,64-4a) |
| D、[4-2a,9-3a]∪(27-3a,64-4a] |
 =1),对于给定的n∈N+,定义
=1),对于给定的n∈N+,定义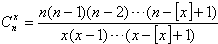 ,x∈[1,+∞),则
,x∈[1,+∞),则 ( ),当x∈[2,3)时,函数
( ),当x∈[2,3)时,函数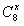 的值域是( )。
的值域是( )。