题目内容
9.(1)设全集U={不大于20的质数},且A∩(∁UB)={3,5},(∁UA)∩B={7,11},(∁UA)∩(∁UB)={2,17},请绘制韦恩图求出集合A,B;(2)利用(1)题中的韦恩图解决下面问题:
向50名学生调查对A,B两观点的态度,结果如下:赞成观点A的人数是全体的$\frac{3}{5}$,其余的不赞成;赞成观点B的比赞成观点A的多3人,其余的不赞成;另外,对观点A,B都不赞成的学生比对观点A,B都赞成的学生的$\frac{1}{3}$多1人.问:对观点A,B都赞成的学生有多少人?
分析 (1)画出韦恩图,即可直接求出集合A和B.
(2)设对A、B都赞成的学生人数为x,则对A、B都不赞成的学生人数为$\frac{x}{3}$+1,赞成A而不赞成B的人数为30-x,赞成B而不赞成A的人数为33-x.依题意(30-x)+(33-x)+x+$\frac{x}{3}$+1=50,解得即可.
解答 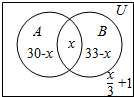 解:(1):∵全集U={x|x取不大于20的质数}={2,3,5,7,11,13,17,19},
解:(1):∵全集U={x|x取不大于20的质数}={2,3,5,7,11,13,17,19},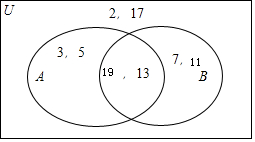
A∩(∁UB)={3,5},(∁UA)∩B={7,11},(∁UA)∩(∁UB)={2,17},
∴由韦恩图可知A={3,5,11,13},B={7,11,13,19}.
(2)赞成A的人数为50×$\frac{3}{5}$=30,赞成B的人数为30+3=33,
如图,记50名学生组成的集合为U,赞成A的学生全体为集合A,赞成B的学生全体为集合B.
设对A、B都赞成的学生人数为x,则对A、B都不赞成的学生人数为$\frac{x}{3}$+1,赞成A而不赞成B的人数为30-x,赞成B而不赞成A的人数为33-x.
依题意(30-x)+(33-x)+x+$\frac{x}{3}$+1=50,解得x=21.
故对观点A,B都赞成的学生有21人.
点评 本题考查利用集合的运算表示韦恩图中的集合、考查利用交集、补集的定义求集合的交集、补集,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
19.已知一组数据为-1,0,3,5,x.它们的方差为6.8,则x的值为( )
| A. | -2或5.5 | B. | 2或-5.5 | C. | 4或11 | D. | -4或-11 |
4.设复数$\frac{1-i}{2+i}$=x+yi,其中x,y∈R,则x+y=( )
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $-\frac{2}{5}$ |
18.下列四个函数中,最小正周期为π,且关于直线x=-$\frac{5π}{12}$对称的函数是( )
| A. | y=sin($\frac{x}{2}+\frac{π}{3}$) | B. | y=sin($\frac{x}{2}-\frac{π}{3}$) | C. | y=sin(2x-$\frac{π}{3}$) | D. | y=sin(2x+$\frac{π}{3}$) |