Question

2．作出下列函数的图象，并写出函数的定义域：
（1）y=2x；
（2）y=$\frac{1}{x}$；
（3）y=x²，x∈[-1，2]；
（4）y=-x+1．

Answer 1

分析 根据正比例函数、一次函数与二次函数以及反比例函数的图象与性质，在坐标系内画出它们的图象即可．

解答 解：（1）函数y=2x的图象是一条过原点的直线，且过点（1，2），它的定义域是R，
画出图象如图1；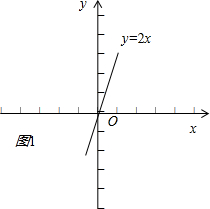
（2）函数y=$\frac{1}{x}$的图象是一、三象限的两支曲线，它的定义域是（-∞，0）∪（0，+∞），
画出图象如图2所示；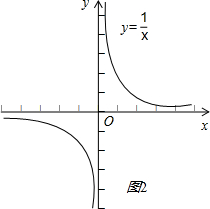
（3）函数y=x²，x∈[-1，2]时的图象是抛物线的一部分，它的定义域是[-1，2]，
画出函数图象如图3所示；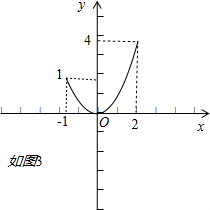
（4）函数y=-x+1的图象是一条直线，且过点（0，1）和（1，0），它的定义域是R，
画出它的图象如图4所示．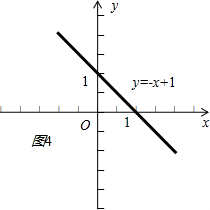

点评 本题考查了正比例函数、反比例函数以及一次函数、二次函数的图象与性质的应用问题，是基础题目．