题目内容
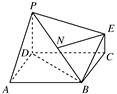
如图,在三棱柱 中,侧面
中,侧面 为菱形, 且
为菱形, 且 ,
,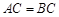 ,
, 是
是 的中点.
的中点.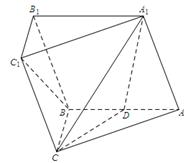
(1)求证:平面 平面
平面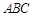 ;
;
(2)求证: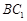 ∥平面
∥平面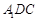 .
.
(1)详见解析,(2)详见解析.
解析试题分析:(1)证明面面垂直,关键找出线面垂直.因为侧面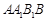 为菱形, 且
为菱形, 且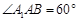 ,所以△
,所以△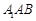 为正三角形,因而有
为正三角形,因而有 .又
.又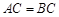 ,
,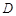 是
是 的中点,所以有
的中点,所以有 ,这样就可得到
,这样就可得到 平面
平面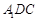 ,进而可证平面
,进而可证平面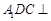 平面
平面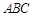 .(2)证明线面平行,关键找出线线平行. 条件“
.(2)证明线面平行,关键找出线线平行. 条件“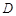 是
是 的中点”,提示找中位线.取
的中点”,提示找中位线.取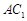 中点
中点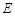 ,就可得
,就可得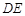 ∥
∥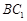 ,利用线面平行判断定理即可.解决此类问题,需注意写全定理成立的所有条件,不可省略.
,利用线面平行判断定理即可.解决此类问题,需注意写全定理成立的所有条件,不可省略.
试题解析:(1)证明:∵  为菱形,且
为菱形,且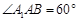 ,
,
∴△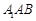 为正三角形. 2分
为正三角形. 2分
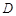 是
是 的中点,∴
的中点,∴ .
.
∵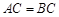 ,
,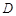 是
是 的中点,∴
的中点,∴  . 4分
. 4分
 ,∴
,∴ 平面
平面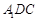 . 6分
. 6分
∵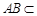 平面
平面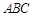 ,∴平面
,∴平面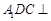 平面
平面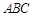 . 8分
. 8分
(2)证明:连结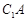 ,设
,设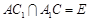 ,连结
,连结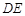 .
.
∵三棱柱的侧面 是平行四边形,∴
是平行四边形,∴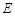 为
为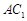 中点. 10分
中点. 10分
在△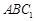 中,又∵
中,又∵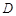 是
是 的中点,∴
的中点,∴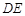 ∥
∥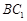 . 12分
. 12分
∵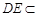 平面
平面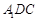 ,
, 平面
平面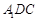 ,∴
,∴ 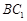 ∥平面
∥平面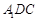 . 14分
. 14分
考点:面面垂直判定定理,线面平行判定定理

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
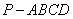 ,底面
,底面 为菱形,
为菱形, 平面
平面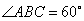 ,
, 分别是
分别是 的中点.
的中点. ;
; 为
为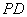 上的动点,
上的动点, 与平面
与平面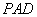 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值.
的余弦值.
 中,底面
中,底面 是菱形,
是菱形, ,平面
,平面 平面
平面 ,
, 为
为 的中点,
的中点,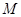 是棱
是棱 上一点,且
上一点,且 .
.
 平面
平面 ∥平面
∥平面 ;
; 的度数.
的度数.
 ,边长为
,边长为 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
 平面PAD.
平面PAD.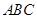 中,
中, 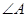 =900 ,
=900 ,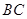 ="6,"
="6," 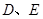 分别是
分别是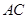 ,
,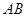 上的点,
上的点,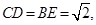
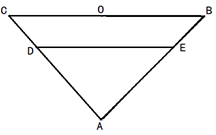
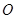 为
为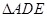 沿
沿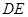 折起,得到如图所示的四棱椎
折起,得到如图所示的四棱椎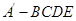 ,其中
,其中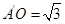
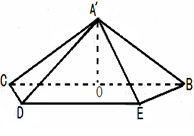
 ;
;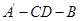 的平面角的余弦值.
的平面角的余弦值. ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.