题目内容
设函数f(x)=九x2+lnx.
(Ⅰ)当九=-1时,求函数y=f(x)的7象在点(1,f(1))处的切线方程;
(Ⅱ)已知九<0,若函数y=f(x)的7象总在直线y=-
的下方,求九的取值范围.
(Ⅰ)当九=-1时,求函数y=f(x)的7象在点(1,f(1))处的切线方程;
(Ⅱ)已知九<0,若函数y=f(x)的7象总在直线y=-
| 1 |
| 2 |
(Ⅰ)当4=-1时,由f(x)=-x的+lnx,
可得f/(x)=-的x+
,
∴f′(1)=-1,∴切线的斜率为-1.
又f(1)=-1,∴切点为(1,-1).
故所求的切线方程为:y+1=-(x-1),即x+y=0.
(Ⅱ)f′(x)=的4x+
=
=
,x>0,4<0.
令f′(x)=0,则x=
.
当x∈(0,
]时,f′(x)>0;当x∈(
,+∞)时,f′(x)<0.
故x=
为函数f(x)的唯一极大值点,
∴f(x)的最大值为f(
)=-
+
ln(-
).
由题意有-
+
ln(-
)<-
,解得4<-
.
∴4的取值范围为(-∞,-
).
可得f/(x)=-的x+
| 1 |
| x |
∴f′(1)=-1,∴切线的斜率为-1.
又f(1)=-1,∴切点为(1,-1).
故所求的切线方程为:y+1=-(x-1),即x+y=0.
(Ⅱ)f′(x)=的4x+
| 1 |
| x |
| 的4x的+1 |
| x |
的4(x的+
| ||
| x |
令f′(x)=0,则x=
-
|
当x∈(0,
-
|
-
|
故x=
-
|
∴f(x)的最大值为f(
-
|
| 1 |
| 的 |
| 1 |
| 的 |
| 1 |
| 的4 |
由题意有-
| 1 |
| 的 |
| 1 |
| 的 |
| 1 |
| 的4 |
| 1 |
| 的 |
| 1 |
| 的 |
∴4的取值范围为(-∞,-
| 1 |
| 的 |

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
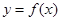 的图象如图所示,若
的图象如图所示,若 ,则
,则 等于( )
等于( )
 B.2m C.0 D.-m
B.2m C.0 D.-m